Under de senaste åren har poker blivit mycket populärt. De flesta källor där man kunde lära sig pokerstrategi, böcker, instruktionsvideor eller annat digitalt innehåll har blivit föråldrade.
Den grundläggande förändringen är att spelare från den gamla skolan tjänade miljoner genom att utnyttja motståndarnas misstag och svagheter. Numera tjänar de stora summorna pengar de som inte bara kan utnyttja sina fördelar och motståndarnas misstag, utan också har en god förståelse för spelteori. Denna faktor lyfter poker till en helt ny nivå.
I denna artikel kommer vi att diskutera:
- Grunderna i spelteori
- Varför du bör använda en spelteoribaserad strategi
- Exempel från Doug Polk, som betonade vikten av spelteori
- 4 skäl till varför det är värt att använda en sådan strategi
Spelteori och poker
John Nash utvecklade spelteori som en gren av matematiken vid Princeton University omkring 1950. Under de senaste 15 åren har poker blivit mycket populärt, och spelarna har nått en mycket hög färdighetsnivå. På denna nivå är det mycket svårt att vara en bra spelare och vinna utan hjälp av spelteori.
En matematisk förståelse har gjort spelet mycket djupare och mer komplext. Baserat på spelteori måste du överväga alla beslut från varje öppning från olika positioner till en till synes obetydlig check på river när du spelar för en liten pott. Varje beslut påverkar hur mycket du vinner och förlorar (win rate) som pokerspelare. Dessa saker mäts i värde som vi förväntar oss eller EV (expected value). Om ditt beslut är lönsamt är det EV+, om inte – EV-.
Ett mycket enkelt exempel på tillämpning av spelteori är när en spelare använder ett specifikt öppningsrange från UTG-positionen.
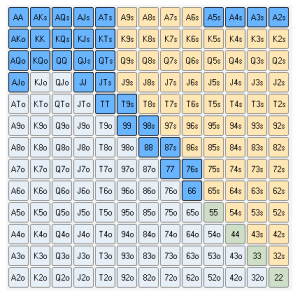
Naturligtvis är det uppenbart att spela mycket starka händer genom att öppna från UTG är ett lönsamt beslut, men om vi bara spelar med de starkaste händerna blir vi mycket förutsägbara. Genom att öppna händer som 9s8s eller 66 balanserar vi vårt öppningsrange och gör spelet svårare för våra motståndare. På detta sätt kan vi samla en stark kombination oavsett om höga, låga eller medelhöga kort vänds på bordet.
Till exempel skulle våra tidigare nämnda kort passa:

Varför använda GTO (game theory optimal)?
Du undrar förmodligen varför denna teori behövs om de flesta pengar kommer från att utnyttja svagare spelares svagheter?
Här är två huvudskäl:
- Genom att använda GTO kommer du att vinna pengar på lång sikt oavsett om du spelar mot svaga eller mer skickliga spelare
- Det är mycket enklare att anpassa och ändra din strategi beroende på motståndarna när du har en grund att utgå från och avvika från beroende på motståndaren
Om du ser på spelet genom GTO-prismen kan du granska dina spelade händer och ta reda på vilket beslut som skulle vara det mest optimala, så att du kan utvärdera ditt spel mer objektivt. Detta perspektiv ger dig möjlighet att förstå om du balanserar ditt range. Dessutom analyserar du inte bara en specifik situation där specifika två kort delas ut, utan får också en allmän förståelse för hur du ska spela i sådana situationer med alla andra kort.
Om du i en situation satsar för värde, måste ditt range också innehålla sådana kort som du skulle bluffa med i samma position, så att din motståndare aldrig kan vara säker på om du bluffar eller har en stark kombination. Om du bara satsar på river när du har en stark hand, kan motståndaren alltid folda lönsamt eftersom han vet att du aldrig bluffar i en sådan situation. Å andra sidan, om du bluffar för ofta i sådana situationer, kan motståndaren alltid syna lönsamt eftersom han vet att du nästan aldrig har en stark kombination.
Om du fortfarande inte tror att en GTO-baserad strategi är vägen att gå, borde dessa hypotetiska exempel från Doug Polk hjälpa.
Pokerteori, exempel
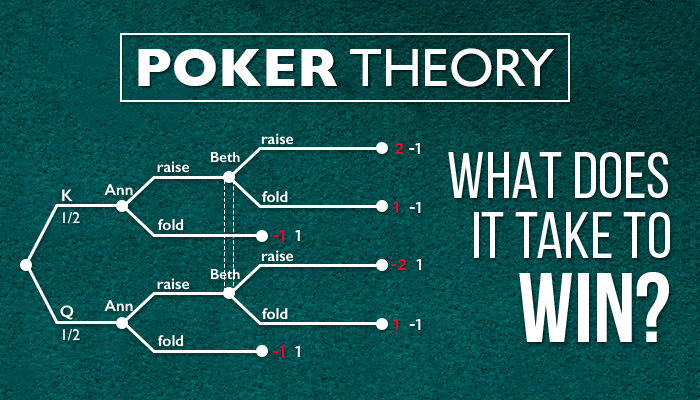
På river satsar du 100 dollar i en 100-dollars pott, så din motståndare måste syna 100 för att vinna 200-potten. Detta innebär att din motståndare har 2 till 1 pot odds och måste vinna minst 33% av gångerna för att gå jämnt upp.
Denna korta beräkning visar den optimala bluffprocenten i ditt range när du satsar på river. Så, 33% innebär att en gång av tre bluffar du, och två gånger satsar du för värde. Denna frekvens är optimal eftersom du oftast vinner potten och inte riskerar att bli genomskådad.
Låt oss titta på 4 olika scenarier för förhållandet mellan värdesatsningar och bluffar, detta kommer att hjälpa till att förstå varför ett range med 33% bluffar och 67% värdesatsningar är optimalt och varför dina motståndare inte kan göra något åt det.
För att förenkla scenarierna, låt oss föreställa oss att vi alltid vinner när motståndaren synar vår värdesatsning och alltid förlorar när han synar en bluff.
Scenario 1 – 0% bluff, 100% värdesatsning
Din motståndare kan folda 100% av gångerna. I dina resultat kommer detta att återspeglas så att du vinner 100 dollar med ditt satsningsrange.
Scenario 2 – 100% bluff, 0% värdesatsning
Din motståndare kan syna 100% av gångerna. I dina resultat kommer detta att återspeglas så att du förlorar 100 dollar med ditt satsningsrange.
Scenario 3 – 50% bluff, 50% värdesatsning
Om din motståndare synar 100% av gångerna, vinner du 200 dollar varje gång du satsar för värde och förlorar 100 dollar när du bluffar. I dina resultat kommer detta att återspeglas så att du vinner 50 dollar om motståndaren alltid synar. (50% * -$100 = -$50; 50% * $200 = $100. $100 – $50 = $50).
Om motståndaren alltid foldar, vinner du 100 dollar (samma som i första scenariot)
Detta scenario visar att det är lika lönsamt att inte bluffa alls som att bluffa 50% av gångerna.
Scenario 4 – 33% bluff, 67% värdesatsning
Om din motståndare alltid synar, vinner du 200 dollar när du satsar för värde och förlorar 100 dollar varje gång du bluffar. I detta fall förlorar du 100 dollar bara 33% av gångerna och vinner 200 dollar 67% av gångerna, vilket innebär att din vinst är 100 dollar. (33% * $100 = -$33; 67% * $200 = $133. $133 – $33 = $100).
Detta förhållande mellan bluffar och värdesatsningar är optimalt eftersom:
- Du vinner 100 dollar om din motståndare alltid synar
- Du vinner 100 dollar om din motståndare alltid foldar
Så, du tjänar 100 dollar oavsett vad din motståndare gör. Naturligtvis är detta win-win-scenario möjligt endast när ditt range är perfekt balanserat. Så, det spelar ingen roll vad din motståndare väljer, eftersom du tjänar lika mycket i båda fallen.
Att tillämpa en sådan balans med hänsyn till motståndarnas misstag och svagheter kan vara ännu mer lönsamt, men det kräver pålitlig information om motståndaren och korrekt tillämpning. Om du vill klättra i nivåer och krossa motståndarna på lång sikt är GTO ett måste.
4 skäl till varför det är värt att använda denna strategi
Låt oss titta på fördelarna med GTO i vår strategi, 4 saker du kommer att uppnå genom att inkludera denna teori i ditt spel.
Du undviker ologiskt tänkande
90-talets pokerutbildning lämnade efter sig ett arv av att försöka förstå på vilken nivå en spelare spelar.
- Nivån där spelaren bara tänker på sin egen hand
- Sedan börjar man fundera på vad motståndaren kan ha
- Nästa nivå är att fundera på vad motståndaren tänker om dina kort
- Sedan börjar man tänka på vad du tänker om vad motståndaren tänker att du har
- Och så vidare.
Idealiskt sett, på något sätt, listar du ut var tänkandet slutar, bestämmer vilken nivå motståndaren är på och anpassar dig därefter. Men verkligheten är annorlunda och att bestämma nivån när man spelar mot en svag spelare är mycket opålitligt. Och mot bra och erfarna spelare kan denna process teoretiskt fortsätta till världens ände tills någon överlistar den andra.
Här är ett utmärkt exempel där två pokerlegender nivåar varandra.
https://www.youtube.com/watch?v=-hVwpaDH0Xo
Jag skulle aldrig ifrågasätta Patrik Antonius pokerfärdigheter, men sådana situationer kan undvikas genom att basera din bluffstrategi på GTO, vilket hjälper dig att undvika nivåkrig som orsakar förvirring och leder till situationer där du bluffar utan equity.
Du undviker felaktiga antaganden
En annan fördel – när du ser på spelet genom GTO-prismen, undviker du felaktiga antaganden om andra spelare. Självklart är vissa antaganden möjliga om du har spelat tillräckligt många händer mot en specifik spelare, men mycket generella antaganden kan kosta mycket.
Till exempel, det skulle inte vara klokt att säga “här kommer det ALDRIG att vara en bluff” eller “han kommer ALLTID att bluffa här”. Du bör inte heller tänka att en okänd motståndare inte kan ha en specifik hand i sin range eller att han öppnar mycket smalt eller mycket brett.
En välstrukturerad GTO-strategi eliminerar förvirring från ditt spel och hjälper dig att spela lönsam poker på lång sikt.
Objektiv analys
De flesta spelare dömer sig själva för att ha spelat en hand dåligt bara för att de inte lyckades vinna den. Men när man utvecklas och går pokerkarriärens väg börjar man förstå att poker inte är en verksamhet där resultaten kan bedömas i ett vakuum.
Att tänka objektivt kan vara mycket svårt, särskilt när resultatet av en spelad hand är mycket dåligt eller mycket bra. Det faktum att du fångade en full house på river och vann många marker från din motståndare betyder inte att det var ett bra spel att syna motståndarens satsning två gånger.
När du har fastställt vilket beslut som är mest lönsamt enligt GTO i en specifik situation, inkludera handen i din sessionsanalys för att ta reda på om du tog ett lönsamt beslut på lång sikt, inte med en specifik hand, utan med din range.
Alla framgångsrika pokerspelare vet att det är nödvändigt att erkänna sina egna misstag om man vill spela bra. GTO ger grunden som gör det mycket lättare att upptäcka misstag.
Enklare anpassning
Varför är teori viktigt när man försöker anpassa sig till andra spelare? För att göra det enklare, låt oss spela ett spel.
Föreställ dig att du har glömt allt du visste om pokerstrategi, förutom grundläggande kunskaper om spelet, och du spelar din första hand i ditt liv.
Live-spel, blinds $1/$2, effektiv stack $200.
Hjälten får Ad9d och är i BB-positionen. Alla foldar till BTN, BTN höjer till $7. SB lägger sig, hjälten synar.
Floppen (potten $14) As Td 3h
Hjälten checkar, BTN satsar $9, hjälten synar.
Turn (potten $32) Jc
Hjälten checkar, BTN satsar $21, hjälten synar.
River (potten $74) 9c
Hjälten checkar, BTN satsar $50, hjälten synar.
BTN visar Ah 2c. Hjälten vinner $174 med två par.
Vad kommer du att göra nästa gång du möter denna spelare i en sådan situation, hur kan du ändra ditt spel för att utnyttja motståndarens svaghet? Utan någon teoretisk förståelse för denna situation kommer du inte att veta var du ska börja.
Å andra sidan, om du vet hur man teoretiskt bäst spelar med A2o i BTN-positionen, kommer du också att veta hur din motståndare avviker från detta. Denna kunskap förenklar anpassningen till denna motståndare.
Här är specifika ändringar vi kan göra för att krossa en aggressiv thin value motståndares strategi.
- Liten exploatering. Syna motståndarens satsningar bredare (med svagare kombinationer än vanligt) på alla gator när han satsar. (överdriv inte)
- Stor exploatering. Attackera obarmhärtigt hans checkande range när han uppenbarligen är mycket svag, med stora satsningar både med thin value och med en rimlig mängd bluffar.
Mycket ofta hjälper förståelsen av optimal spelteori att lättare utnyttja motståndarnas svagheter eftersom du exakt vet var din motståndares beslut avviker från det optimala spelet. När du inte vet vad som är bra är det nästan omöjligt att förstå vad som är dåligt.
Sammanfattning
Att sträva efter en perfekt GTO-strategi kan verka som en logisk slutsats, men sanningen är att ingen kan spela perfekt enligt denna teori. Poker kommer någon gång att lösas av en människa eller maskin, men vi rekommenderar ändå att basera ditt spel på denna teori så mycket som möjligt. Som alltid betyder det att du måste arbeta med ditt spel både när du spelar och efter spelstunden.
Denna artikel är bara en sammanfattning av de grundläggande principerna för spelteori som tillämpas i poker, men vi hoppas att du har fått något användbart eller åtminstone väckt din nyfikenhet – hur du kan berika ditt spel genom att tillämpa spelteori.