En los últimos años, el póker se ha vuelto muy popular. La mayoría de las fuentes de las que se podía aprender estrategias de póker, libros, videos educativos u otro contenido digital han quedado obsoletas.
El cambio fundamental es que los jugadores de la vieja escuela acumularon millones al aprovechar los errores y debilidades de sus oponentes. Hoy en día, quienes ganan grandes sumas de dinero no solo aprovechan sus ventajas y los errores de sus oponentes, sino que también comprenden bien la teoría del juego. Este factor eleva el póker a un nivel completamente diferente.
En este artículo discutiremos:
- Los fundamentos de la teoría del juego
- Por qué deberías usar una estrategia basada en la teoría del juego
- Ejemplos de Doug Polk, quien destacó la importancia de la teoría del juego
- 4 razones por las que vale la pena usar esta estrategia
Teoría del juego y póker
John Nash desarrolló la teoría del juego como una rama de las matemáticas en la Universidad de Princeton alrededor de 1950. En 15 años, el póker se volvió muy popular y los jugadores alcanzaron un nivel de habilidad muy alto. En este nivel, es muy difícil ser un buen jugador y ganar sin la ayuda de la teoría del juego.
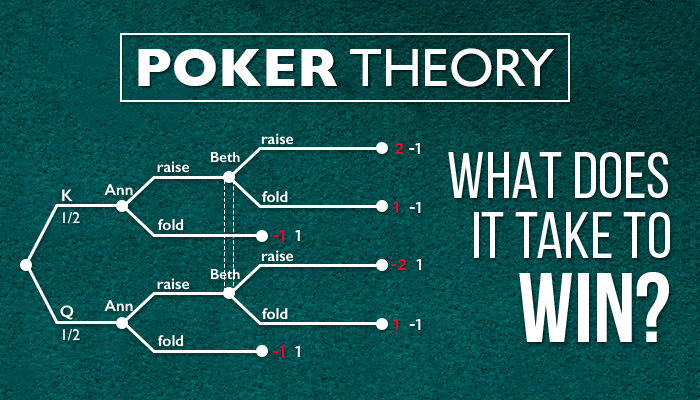
La comprensión matemática hizo que el juego fuera mucho más profundo y complejo. Basándote en la teoría del juego, debes considerar todas las decisiones, desde cada apertura en diferentes posiciones hasta un aparentemente insignificante check en el river jugando por un bote pequeño. Cada decisión determina cuánto ganas y cuánto pierdes (win rate) como jugador de póker. Estas cosas se miden en valor esperado o EV (expected value). Si tu decisión es rentable, es EV+, si no lo es, es EV-.
Un ejemplo muy simple de la aplicación de la teoría del juego es que un jugador usa un range específico de apertura desde la posición UTG.
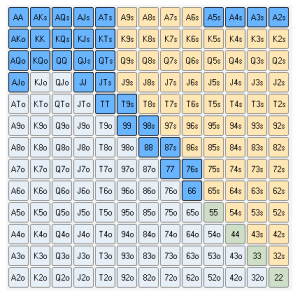
Por supuesto, es obvio que jugar manos muy fuertes abriendo desde UTG es una decisión rentable, pero si solo jugáramos con las manos más fuertes, seríamos muy predecibles. Al abrir manos como 9s8s o 66, equilibramos nuestro range de apertura y dificultamos el juego para nuestros oponentes. De esta manera, podemos formar una combinación fuerte independientemente de si las cartas en la mesa son altas, bajas o medianas.
Por ejemplo, nuestras cartas mencionadas anteriormente serían adecuadas para:

¿Por qué vale la pena usar GTO (game theory optimal)?
Probablemente te estés preguntando, ¿para qué sirve esta teoría si la mayor parte del dinero proviene de aprovechar las debilidades de los jugadores más débiles?
Aquí hay dos razones principales:
- Usando GTO a largo plazo ganarás dinero independientemente de si juegas contra jugadores débiles o más hábiles
- Adaptarse y cambiar tu estrategia según los oponentes es mucho más fácil cuando tienes una base desde la cual desviarte dependiendo del oponente
Si miras el juego a través del prisma de GTO, puedes revisar tus manos jugadas y determinar cuál sería la decisión más óptima, por lo tanto, puedes evaluar tu juego de manera más objetiva. Este punto de vista te permite entender si estás equilibrando tu range. Además, no solo analizas una situación específica en la que se reparten dos cartas específicas, sino que en general obtienes una comprensión de cómo jugar en esa situación con todas las demás cartas.
Si en una situación haces una apuesta por valor, tu range debe incluir cartas con las que también farolearías en la misma posición, de modo que tu oponente nunca pueda estar seguro de si estás faroleando o tienes una combinación fuerte. Si solo apuestas en el river cuando tienes una mano fuerte, tu oponente siempre puede retirarse de manera rentable porque sabe que nunca faroleas en esa situación. Por otro lado, si faroleas demasiado en esas situaciones, tu oponente siempre puede pagar de manera rentable porque sabe que casi nunca tienes una combinación fuerte.
Si aún no crees que una estrategia basada en GTO es el camino a seguir, estos ejemplos hipotéticos de Doug Polk deberían ayudar.
Teoría del póker, ejemplos
En el river, apuestas 100 dólares en un bote de 100 dólares, por lo que tu oponente necesita pagar 100 para ganar un bote de 200. Esto significa que tu oponente tiene 2 a 1 pot odds y necesita ganar al menos el 33% de las veces para estar even.
Este breve cálculo muestra la proporción óptima de faroles en tu range cuando apuestas en el river. Entonces, el 33% significa que una de cada tres veces estarás faroleando y dos veces estarás apostando por valor. Esta frecuencia es óptima porque generalmente ganarás el bote y no correrás el riesgo de ser descubierto.
Veamos 4 escenarios diferentes de proporción de apuestas por valor y faroles, esto ayudará a entender por qué un range con 33% de faroles y 67% de apuestas por valor es óptimo y por qué tus oponentes no podrán hacer nada contra ti.
Para simplificar los escenarios, imaginemos que siempre ganamos cuando el oponente paga nuestra apuesta por valor y siempre perdemos cuando paga nuestro farol.
Escenario 1 – 0% farol, 100% apuesta por valor
Tu oponente puede retirarse el 100% de las veces. En tus resultados, esto se reflejará como ganar 100 dólares con tu range de apuestas.
Escenario 2 – 100% farol, 0% apuesta por valor
Tu oponente puede pagar el 100% de las veces. En tus resultados, esto se reflejará como perder 100 dólares con tu range de apuestas.
Escenario 3 – 50% farol, 50% apuesta por valor
Si tu oponente paga el 100% de las veces, ganarás 200 dólares siempre que apuestes por valor y perderás 100 dólares cuando farolees. En tus resultados, esto se reflejará como ganar 50 dólares si el oponente siempre paga. (50% * -$100 = -$50; 50% * $200 = $100. $100 – $50 = $50).
Si el oponente siempre se retira, ganarás 100 dólares (igual que en el primer escenario).
Este escenario muestra que no farolear en absoluto es tan rentable como farolear el 50% de las veces.
Escenario 4 – 33% farol, 67% apuesta por valor
Si tu oponente siempre paga, ganarás 200 dólares cuando apuestes por valor y perderás 100 dólares siempre que farolees. En este caso, perderás 100 dólares solo el 33% de las veces y ganarás 200 dólares el 67% de las veces, lo que significa que tu ganancia es de 100 dólares. (33% * $100 = -$33; 67% * $200 = $133. $133 – $33 = $100).
Esta proporción de faroles y apuestas por valor es óptima porque:
- Ganas 100 dólares si tu oponente siempre paga
- Ganas 100 dólares si tu oponente siempre se retira
Así que, ganas 100 dólares independientemente de lo que haga tu oponente. Por supuesto, este escenario de ganar-ganar solo es posible cuando tu range está perfectamente equilibrado. Por lo tanto, no te importa lo que elija tu oponente, ya que en ambos casos ganas lo mismo.
Aplicar este equilibrio teniendo en cuenta los errores y debilidades de los oponentes puede ser aún más rentable, pero necesitas información confiable sobre el oponente y una aplicación correcta. Si deseas subir de límites y aplastar a tus oponentes a largo plazo, GTO es esencial.
4 razones por las que vale la pena usar esta estrategia
Revisemos los beneficios de GTO en nuestra estrategia, 4 cosas que lograrás al incorporar esta teoría en tu juego.
Evitarás pensamientos ilógicos
El legado de los entrenamientos de póker de los 90 es intentar entender en qué nivel juega el jugador.
- Nivel en el que el jugador solo piensa en su propia mano
- Luego comienza a considerar lo que podría tener el oponente
- El siguiente nivel es pensar en lo que el oponente piensa sobre tus cartas
- Luego comienza a pensar en lo que tú piensas sobre lo que el oponente piensa que tú tienes
- Y así sucesivamente.
Idealmente, de alguna manera descubres en qué nivel termina el pensamiento, determinas en qué nivel está el oponente y te adaptas en consecuencia. Pero la realidad es diferente y determinar el nivel jugando contra un jugador débil es muy poco confiable. Y contra buenos y experimentados jugadores, este proceso teóricamente puede continuar hasta el fin del mundo, hasta que uno de los dos sobrepiense al otro.
Aquí hay un excelente ejemplo donde dos leyendas del póker se nivelan mutuamente.
https://www.youtube.com/watch?v=-hVwpaDH0Xo
Nunca cuestionaría las habilidades de Patrik Antonius en el póker, pero tales situaciones se pueden evitar basando tu estrategia de faroles en GTO, lo que te ayudará a no involucrarte en guerras de niveles que causan confusión y te llevan a situaciones en las que faroleas sin tener equity.
Evitarás suposiciones erróneas
Otra ventaja es que, al mirar el juego a través del prisma de GTO, evitas hacer suposiciones erróneas sobre otros jugadores. Por supuesto, algunas suposiciones son posibles si tienes más que suficientes manos jugadas contra un jugador en particular, pero las suposiciones muy generalizadas pueden costar mucho.
Por ejemplo, no sería inteligente decir “aquí NUNCA habrá un farol” o “él SIEMPRE faroleará aquí”. Tampoco deberías pensar que un oponente desconocido no puede tener una mano específica en su rango o que abre muy estrecho o muy amplio.
Una estrategia GTO bien estructurada elimina la confusión de tu juego y te ayuda a jugar al póker de manera rentable a largo plazo.
Análisis objetivo
La mayoría de los jugadores se juzgan a sí mismos por haber jugado mal una mano solo porque no lograron ganarla. Sin embargo, a medida que mejoras y avanzas en tu carrera de póker, comienzas a entender que el póker no es un negocio cuyos resultados se puedan evaluar en un vacío.
Pensar objetivamente puede ser muy difícil, especialmente cuando el resultado de una mano jugada es muy malo o muy bueno. El hecho de que hayas conseguido un full house en el river y ganado muchas fichas de tu oponente no significa que haber pagado dos veces la apuesta del oponente haya sido una buena jugada.
Cuando descubres cuál es la decisión más rentable según GTO en una situación específica, incluye la mano en tu análisis de sesión para saber si tomaste una decisión rentable a largo plazo, no con una mano específica, sino con tu rango.
Todos los jugadores de póker exitosos saben que admitir tus propios errores es esencial si quieres jugar bien. GTO proporciona una base que facilita mucho la detección de errores.
Adaptación más sencilla
¿Por qué es importante la teoría al intentar adaptarse a otros jugadores? Para simplificar, juguemos un juego.
Imagina que has olvidado todo lo que sabías sobre la estrategia de póker, excepto los conocimientos básicos del juego, y estás jugando tu primera mano en tu vida.
Juego en vivo, ciegas $1/$2, stack efectivo $200.
El héroe recibe Ad9d y está en la posición de BB. Todos foldean hasta el BTN, el BTN sube a $7. El SB tira las cartas, el héroe paga.
Flop (bote $14) As Td 3h
El héroe pasa, el BTN apuesta $9, el héroe paga.
Turn (bote $32) Jc
El héroe pasa, el BTN apuesta $21, el héroe paga.
River (bote $74) 9c
El héroe pasa, el BTN apuesta $50, el héroe paga.
El BTN muestra Ah 2c. El héroe gana $174 con dos pares.
¿Qué harás la próxima vez que te enfrentes a este jugador en una situación similar? ¿Cómo puedes cambiar tu juego para explotar la debilidad del oponente? Sin ningún entendimiento teórico de esta situación, no sabrás por dónde empezar.
Por otro lado, si sabes cómo jugar teóricamente mejor con A2o en la posición de BTN, también sabrás cómo se desvió tu oponente de eso. Este conocimiento simplifica el camino para adaptarse a este oponente.
Aquí hay cambios específicos que podemos hacer para aplastar la estrategia agresiva de thin value del oponente.
- Explotación pequeña. Paga las apuestas del oponente más ampliamente (con combinaciones más débiles de lo habitual) en todas las calles cuando él hace apuestas. (no te excedas)
- Explotación grande. Ataca implacablemente su rango de check cuando está claramente muy débil, con grandes apuestas tanto con thin value como con una cantidad razonable de faroles.
Muy a menudo, comprender la teoría del juego óptimo facilita la explotación de las debilidades de los oponentes porque sabes exactamente dónde se desvían las decisiones de tu oponente del juego óptimo. Cuando no sabes qué es lo correcto, es casi imposible entender qué es lo incorrecto.
Resumamos
Buscar una estrategia GTO perfecta puede parecer una conclusión lógica, pero la verdad es que nadie puede jugar perfectamente según esta teoría. El póker será resuelto algún día por un humano o una máquina, pero aún así recomendamos basar tu juego en esta teoría tanto como sea posible. Como siempre, esto significa que debes trabajar en tu juego tanto jugando como fuera de las horas de juego.
Este artículo solo resume los fundamentos de la teoría del juego aplicados al póker, pero esperamos que hayas encontrado algo útil o al menos hayas despertado tu curiosidad sobre cómo enriquecer tu juego aplicando la teoría del juego.