Pēdējo gadu laikā pokers ir kļuvis ļoti populārs. Lielākā daļa avotu, no kuriem varēja mācīties pokera stratēģiju, grāmatas, mācību video vai cits digitālais saturs ir novecojuši.
Būtiskās izmaiņas ir tādas, ka vecās skolas spēlētāji nopelnīja miljonus, izmantojot pretinieku kļūdas un vājās vietas. Mūsdienās lielas naudas summas pelna tie, kuri ne tikai spēj izmantot savas priekšrocības un pretinieku kļūdas, bet arī labi izprot spēles teoriju. Šis faktors paceļ pokeru pavisam citā līmenī.
Šajā rakstā apspriedīsim:
- Spēles teorijas pamatus
- Kāpēc jums vajadzētu izmantot uz spēles teoriju balstītu stratēģiju
- Doug Polk piemērus, kas izcēla spēles teorijas nozīmi
- 4 iemeslus, kāpēc ir vērts izmantot šādu stratēģiju
Spēles teorija un pokers
John Nash izveidoja spēles teoriju kā matemātikas nozari Prinstonas universitātē ap 1950. gadu. Pēdējo 15 gadu laikā pokers ir kļuvis ļoti populārs, un spēlētāji ir sasnieguši ļoti augstu prasmju līmeni. Šādā līmenī ir ļoti grūti būt labam spēlētājam un uzvarēt bez spēles teorijas palīdzības.
Matemātiskā izpratne padarīja spēli daudz dziļāku un sarežģītāku. Balstoties uz spēles teoriju, jums ir jāapsver visi lēmumi, sākot no katras pozīcijas atvēršanas līdz šķietami nenozīmīgam check riverā, spēlējot par mazu banku. Katrs lēmums ietekmē to, cik daudz jūs uzvarat un cik daudz zaudējat (win rate) kā pokera spēlētājs. Šīs lietas tiek mērītas ar vērtību, kuru sagaidām, vai EV (expected value). Ja jūsu pieņemtais lēmums ir ienesīgs, tas ir EV+, ja nē – EV-.
Ļoti vienkāršs spēles teorijas piemērs ir spēlētājs, kurš izmanto konkrētu atvēršanas range no UTG pozīcijas.
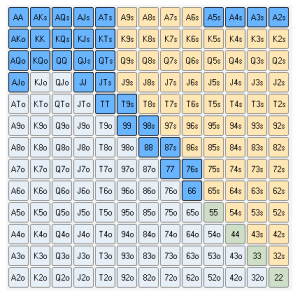
Protams, ir acīmredzami, ka ļoti stipras rokas spēlēt, atverot no UTG, ir ienesīgs lēmums, taču, ja mēs spēlētu tikai ar pašām stiprākajām rokām, mēs būtu ļoti paredzami. Atverot tādas rokas kā 9s8s vai 66, mēs līdzsvarojam savu atvēršanas range un apgrūtinām spēli saviem pretiniekiem. Tādā veidā mēs varam savākt stipru kombināciju neatkarīgi no tā, vai uz galda būs augstas, zemas vai vidējas kārtis.
Piemēram, mūsu iepriekš minētajām kārtīm būtu piemērotas:

Kāpēc ir vērts izmantot GTO (game theory optimal)?
Iespējams, jūs domājat, kāpēc šī teorija ir nepieciešama, ja lielākā daļa naudas nāk no tā, ka spējat izmantot vājāku spēlētāju vājās vietas?
Šeit ir divi galvenie iemesli:
- Izmantojot GTO ilgtermiņā, jūs uzvarēsiet naudu neatkarīgi no tā, vai spēlējat pret vājiem vai prasmīgākiem spēlētājiem
- Pielāgoties un mainīt savu stratēģiju atkarībā no pretiniekiem ir daudz vienkāršāk, ja jums ir kāds pamats, no kura novirzīties vienā vai otrā virzienā atkarībā no pretinieka
Ja jūs skatāties uz spēli caur GTO prizmu, jūs varat pārskatīt savas spēlētās rokas un noskaidrot, kurš lēmums būtu visoptimālākais, tādējādi jūs varat objektīvāk novērtēt savu spēli. Šāds skatījums dod iespēju saprast, vai līdzsvarojat savu range. Turklāt jūs analizējat ne tikai vienu konkrētu situāciju, kurā tiek izdalītas konkrētas divas kārtis, bet arī vispārīgi saprotat, kā šādā situācijā būtu jāspēlē ar visām citām kārtīm.
Ja vienā situācijā veicat likmi vērtības dēļ, tad jūsu range ir jābūt arī tādām kārtīm, ar kurām tajā pašā vietā blefotu, lai jūsu pretinieks nekad nevarētu būt pārliecināts, vai jūs blefojat vai jums ir stipra kombinācija. Ja jūs liekat riverā tikai tad, kad jums ir stipra kombinācija, pretinieks vienmēr var izdevīgi foldot, jo zina, ka jūs šādā situācijā nekad neblefojat. No otras puses, ja šādās situācijās blefojat pārāk bieži, pretinieks vienmēr var izdevīgi atbildēt, jo zina, ka gandrīz nekad jums nav stipras kombinācijas.
Ja jūs joprojām nedomājat, ka uz GTO balstīta stratēģija ir ceļš, pa kuru vajadzētu iet, šie hipotētiskie Doug Polk piemēri varētu palīdzēt.
Pokera teorija, piemēri
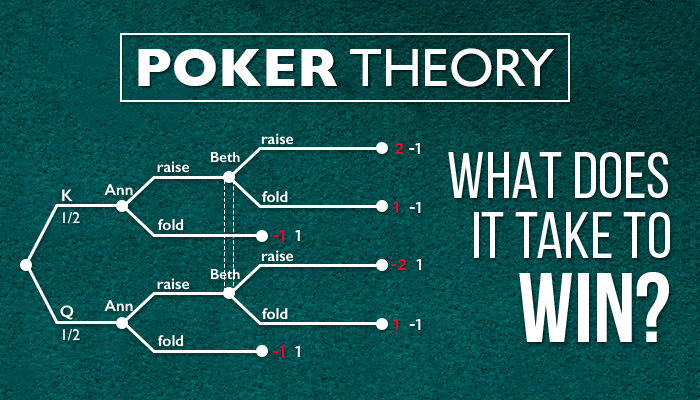
Riverā jūs liekat 100 dolārus 100 dolāru bankā, tāpēc jūsu pretiniekam ir jāatbild ar 100 dolāriem, lai laimētu 200 dolāru banku. Tas nozīmē, ka jūsu pretiniekam ir 2 pret 1 pot odds un viņam ir jāuzvar vismaz 33% gadījumu, lai būtu uz nulles.
Šis īsais aprēķins parāda optimālo blefu proporciju jūsu range, kad liekat riverā. Tātad, 33% nozīmē, ka vienu reizi no trim jūs blefojat, bet divas reizes liekat vērtības dēļ. Šāds biežums ir optimāls, jo bieži vien uzvarēsiet banku un neriskēsiet tikt pārspēti.
Apskatīsim 4 dažādus likmju vērtības un blefu attiecības scenārijus, tas palīdzēs saprast, kāpēc range ar 33% blefu un 67% likmju vērtības dēļ ir optimāls un kāpēc jūsu pretinieki neko jums nevarēs izdarīt.
Scenāriji ir vienkāršoti, iedomāsimies, ka vienmēr uzvaram, kad pretinieks atbild uz mūsu likmi vērtības dēļ, un vienmēr zaudējam, kad atbild uz blefu.
1. scenārijs – blefs 0%, likme vērtības dēļ 100%
Jūsu pretinieks var foldot 100% gadījumu. Jūsu rezultātos tas atspoguļosies tā, ka uzvarēsiet 100 dolārus ar savu likmju range.
2. scenārijs – blefs 100%, likme vērtības dēļ 0%
Jūsu pretinieks var atbildēt 100% gadījumu. Jūsu rezultātos tas atspoguļosies tā, ka zaudēsiet 100 dolārus ar savu likmju range.
3. scenārijs – blefs 50%, likme vērtības dēļ 50%
Ja jūsu pretinieks atbild 100% gadījumu, jūs uzvarēsiet 200 dolārus vienmēr, kad liksiet vērtības dēļ, un zaudēsiet 100 dolārus, kad blefosiet. Jūsu rezultātos tas atspoguļosies tā, ka uzvarēsiet 50 dolārus, ja pretinieks vienmēr atbildēs. (50% * -$100 = -$50; 50% * $200 = $100. $100 – $50 = $50).
Ja pretinieks vienmēr foldos, uzvarēsiet 100 dolārus (tāpat kā pirmajā scenārijā).
Šis scenārijs parāda, ka neblefot vispār ir tikpat ienesīgi kā blefot 50% gadījumu.
4. scenārijs – blefs 33%, likme vērtības dēļ 67%
Ja jūsu pretinieks vienmēr atbild, jūs uzvarēsiet 200 dolārus, kad liksiet vērtības dēļ, un zaudēsiet 100 dolārus vienmēr, kad blefosiet. Šajā gadījumā jūs zaudēsiet 100 dolārus tikai 33% gadījumu un uzvarēsiet 200 dolārus 67% gadījumu, tas nozīmē, ka jūsu peļņa būs 100 dolāri. (33% * $100 = -$33; 67% * $200 = $133. $133 – $33 = $100).
Šāda blefu un likmju vērtības dēļ attiecība ir optimāla, jo:
- Jūs uzvarēsiet 100 dolārus, ja jūsu pretinieks vienmēr atbild
- Jūs uzvarēsiet 100 dolārus, ja jūsu pretinieks vienmēr foldo
Tātad, jūs nopelnāt 100 dolārus neatkarīgi no tā, ko dara jūsu pretinieks. Protams, šis win-win scenārijs ir iespējams tikai tad, ja jūsu range ir perfekti līdzsvarots. Tādējādi jums pilnīgi nav svarīgi, ko izvēlas jūsu pretinieks, jo abos gadījumos jūs nopelnāt tikpat.
Šāda līdzsvara pielietošana, ņemot vērā pretinieku kļūdas un vājās vietas, var būt vēl ienesīgāka, taču nepieciešama uzticama informācija par pretinieku un pareiza pielietošana. Ja vēlaties kāpt pa līmeņiem un ilgtermiņā sagraut pretiniekus, GTO ir nepieciešams.
4 iemesli, kāpēc ir vērts izmantot šo stratēģiju
Apskatīsim GTO priekšrocības mūsu stratēģijā, 4 lietas, kuras sasniegsiet, iekļaujot šo teoriju savā spēlē.
Izvairīsieties no nelogiskas domāšanas
90. gadu pokera mācību mantojums – mēģinājums saprast, kādā līmenī spēlē spēlētājs.
- Līmenis, kad spēlētājs domā tikai par savu roku
- Tālāk sāk domāt, ko varētu būt pretiniekam
- Nākamais līmenis – domā par to, ko pretinieks domā par jūsu kārtīm
- Tālāk sāk domāt par to, ko jūs domājat par to, ko pretinieks domā, ka jums ir
- Un tā tālāk.
Ideālā gadījumā jūs kaut kā noskaidrojat, kurā līmenī domāšana beidzas, nosakāt, kurā līmenī ir pretinieks, un attiecīgi pielāgojaties. Bet realitāte ir citāda, un līmeņa noteikšana, spēlējot pret vāju spēlētāju, ir ļoti neuzticama. Un pret labiem un pieredzējušiem spēlētājiem šis process teorētiski var turpināties līdz pasaules galam, kamēr kāds cits pārdomās.
Šeit ir lielisks piemērs, kur divas pokera leģendas līmeņojas.
https://www.youtube.com/watch?v=-hVwpaDH0Xo
Es nekad neapšaubītu Patrik Antonius spējas pokerā, taču šādas situācijas var izvairīties, balstot savu blefošanas stratēģiju uz GTO, kas palīdzēs neiesaistīties līmeņu karos, kas izraisa apjukumu un noved pie situācijām, kad blefojat bez equity.
Izvairīsieties no kļūdainiem pieņēmumiem
Vēl viena priekšrocība – skatoties uz spēli caur GTO prizmu, jūs izvairīsieties no kļūdainiem pieņēmumiem par citiem spēlētājiem. Protams, daži pieņēmumi ir iespējami, ja jums ir vairāk nekā pietiekami daudz izspēlētu roku pret konkrētu spēlētāju, taču ļoti vispārīgi pieņēmumi var izmaksāt daudz.
Piemēram, nebūtu gudri teikt “šeit NEKAD nebūs blefs” vai “viņš VIENMĒR šeit blefos”. Tāpat nevajadzētu domāt, ka nezināms pretinieks nevarētu būt ar konkrētu roku savā range vai ka viņš atveras ļoti šauri vai ļoti plaši.
Labi izstrādāta GTO stratēģija novērš apjukumu no jūsu spēles un palīdz spēlēt ienesīgu pokeru ilgtermiņā.
Objektīva analīze
Lielākā daļa spēlētāju sevi nosoda par to, ka slikti izspēlēja roku, tikai tāpēc, ka neizdevās to uzvarēt. Taču, attīstoties un ejot pa pokera karjeras ceļu, sāk saprast, ka pokers nav tāds bizness, kura rezultātus var vērtēt vakuumā.
Domāt objektīvi var būt ļoti grūti, īpaši, ja izspēlētās rokas rezultāts ir ļoti slikts vai ļoti labs. Tas, ka jūs riverī noķērāt full house un uzvarējāt daudz žetonu no sava pretinieka, nenozīmē, ka divreiz atbildēt uz pretinieka likmi bija labs gājiens.
Kad noskaidrojat, kurš lēmums ir visienesīgākais saskaņā ar GTO konkrētajā situācijā, iekļaujiet roku savā sesijas analīzē, lai uzzinātu, vai pieņēmāt ilgtermiņā ienesīgu lēmumu ne ar konkrētu roku, bet ar savu range.
Visi veiksmīgie pokera spēlētāji zina, ka atzīt savas kļūdas ir būtiski, ja vēlaties spēlēt labi. GTO nodrošina pamatus, kas palīdz daudz vieglāk pamanīt kļūdas.
Vienkāršāka pielāgošanās
Kāpēc teorija ir svarīga, mēģinot pielāgoties citiem spēlētājiem? Lai būtu vienkāršāk, spēlēsim spēli.
Iedomājieties, ka esat aizmirsis visu, ko zinājāt par pokera stratēģiju, izņemot pamatzināšanas par spēli, un jūs spēlējat pirmo roku savā dzīvē.
Dzīva spēle, obligātās likmes $1/$2, efektīvais steks $200.
Varonis saņem Ad9d un ir BB pozīcijā. Visi līdz BTN foldina, BTN paceļ likmes līdz $7. SB izmet kārtis, varonis atbild.
Flops (bankā $14) As Td 3h
Varonis pārbauda, BTN liek $9, varonis atbild.
Turns (bankā $32) Jc
Varonis pārbauda, BTN liek $21, varonis atbild.
Rivers (bankā $74) 9c
Varonis pārbauda, BTN liek $50, varonis atbild.
BTN rāda Ah 2c. Varonis uzvar $174 ar diviem pāriem.
Ko darīsiet nākamreiz, kad sastapsieties ar šo spēlētāju šādā situācijā, kā varat mainīt savu spēli, lai izmantotu pretinieka vājumu? Bez jebkāda teorētiska izpratnes par šo situāciju, jūs nezināsiet, no kurienes sākt.
No otras puses, ja zināt, kā teorētiski vislabāk spēlēt ar A2o BTN pozīcijā, jūs zināsiet arī to, kā jūsu pretinieks no tā novirzījās. Šīs zināšanas vienkāršo pielāgošanās ceļu šim pretiniekam.
Šeit ir specifiskas izmaiņas, kuras varam veikt, lai sagrautu agresīvu thin value pretinieka stratēģiju.
- Mazs izmantošanas veids. Atbildiet uz pretinieka likmēm plašāk (ar vājākām kombinācijām nekā parasti) visās ielās, kad viņš veic likmes. (nepārspīlējiet)
- Liels izmantošanas veids. Nežēlīgi uzbrūkiet viņa pārbaudes range, kad viņš acīmredzami ir ļoti vājš, ar lielām likmēm gan ar thin value, gan ar saprātīgu daudzumu blefu.
Ļoti bieži optimālās spēles teorijas izpratne palīdz vieglāk izmantot pretinieku vājības, jo jūs precīzi zināt, kur no optimālās spēles novirzās jūsu pretinieka lēmumi. Kad nezināt, kas ir labi, gandrīz neiespējami saprast, kas ir slikti.
Apkoposim
Tīras GTO stratēģijas sasniegšana varētu šķist loģisks secinājums, taču patiesība ir tāda, ka neviens nespēj pilnīgi spēlēt saskaņā ar šo teoriju. Pokers kādreiz tiks atrisināts cilvēka vai mašīnas, taču mēs joprojām iesakām spēli balstīt uz šo teoriju, cik vien iespējams. Kā vienmēr, tas nozīmē, ka jums ir jāstrādā ar savu spēli gan spēles laikā, gan pēc spēles stundām.
Šis raksts ir tikai spēles teorijas pamatu kopsavilkums, kas tiek piemērots pokerā, taču ceram, ka arī no tā jūs guvāt kaut ko noderīgu vai vismaz pamodinājāt zinātkāri – kā bagātināt savu spēli, pielāgojot spēles teoriju.