Viime vuosina pokeri on tullut suositummaksi. Useimmat lähteet, joista pokeristrategiaa voitiin oppia, kuten kirjat, opetusvideot tai muu digitaalinen sisältö, ovat vanhentuneet.
Olennaisin muutos on se, että vanhan koulukunnan pelaajat ansaitsivat miljoonia hyödyntämällä vastustajien virheitä ja heikkouksia. Nykyään suuria summia ansaitsevat ne, jotka eivät vain hyödynnä omaa etuaan ja vastustajien virheitä, vaan myös ymmärtävät hyvin peliteoriaa. Tämä tekijä nostaa pokerin aivan uudelle tasolle.
Tässä artikkelissa käsittelemme:
- Peliteorian perusteet
- Miksi sinun pitäisi käyttää peliteoriaan perustuvaa strategiaa
- Doug Polkin esimerkkejä, jotka korostavat peliteorian merkitystä
- 4 syytä, miksi kannattaa käyttää tällaista strategiaa
Peliteoria ja pokeri
John Nash kehitti peliteorian matematiikan haarana Princetonin yliopistossa noin vuonna 1950. Viimeisten 15 vuoden aikana pokeri on tullut erittäin suosituksi, ja pelaajat ovat saavuttaneet erittäin korkean taitotason. Tällaisella tasolla on erittäin vaikeaa olla hyvä pelaaja ja voittaa ilman peliteorian apua.
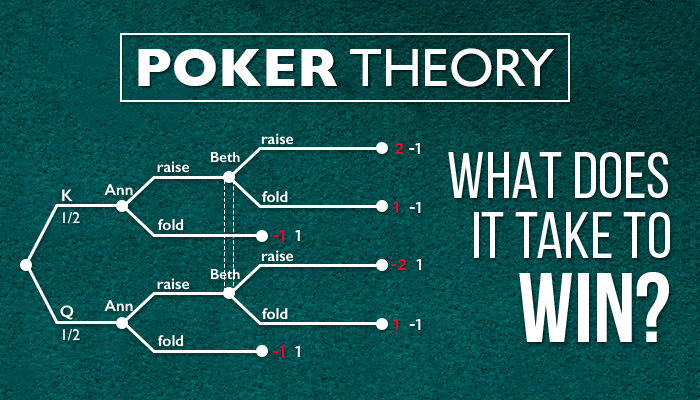
Matemaattinen ymmärrys on tehnyt pelistä paljon syvemmän ja monimutkaisemman. Peliteoriaan perustuen sinun on harkittava kaikkia päätöksiä jokaisesta avauksesta eri positioista aina näennäisesti merkityksettömään checkiin riverillä pelatessasi pientä pottia. Jokainen päätös vaikuttaa siihen, kuinka paljon voitat ja kuinka paljon häviät (win rate) pokerinpelaajana. Nämä asiat mitataan arvolla, jota odotamme tai EV:llä (expected value). Jos päätöksesi on voitollinen, se on EV+, jos ei, se on EV-.
Hyvin yksinkertainen esimerkki peliteorian soveltamisesta on pelaaja, joka käyttää tiettyä avausrangea UTG-positiosta.
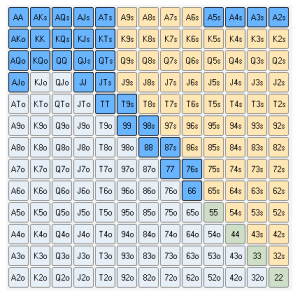
On selvää, että erittäin vahvojen käsien pelaaminen avaamalla UTG:stä on voitollinen päätös, mutta jos pelaisimme vain kaikkein vahvimmilla käsillä, olisimme hyvin ennalta-arvattavia. Avaamalla käsiä kuten 9s8s tai 66 tasapainotamme avausrangemme ja teemme pelistä vaikeampaa vastustajillemme. Näin voimme saada vahvan yhdistelmän riippumatta siitä, ovatko pöytäkortit korkeat, matalat vai keskitasoa.
Esimerkiksi aiemmin mainitsemamme kortit sopisivat seuraaviin tilanteisiin:

Miksi käyttää GTO:ta (game theory optimal)?
Saatat miettiä, miksi tämä teoria on tarpeen, jos suurin osa rahoista tulee siitä, että pystyt hyödyntämään heikompien pelaajien heikkouksia?
Tässä kaksi pääsyytä:
- Käyttämällä GTO:ta pitkällä aikavälillä voitat rahaa riippumatta siitä, pelaatko heikkoja vai taitavampia pelaajia vastaan
- On helpompaa mukauttaa ja muuttaa strategiaasi vastustajien mukaan, kun sinulla on jokin perusta, josta poiketa vastustajan mukaan
Jos katsot peliä GTO:n näkökulmasta, voit tarkastella pelattuja käsiäsi ja selvittää, mikä päätös olisi ollut optimaalinen, joten voit arvioida peliäsi objektiivisemmin. Tällainen näkökulma antaa mahdollisuuden ymmärtää, tasapainotatko rangeasi. Lisäksi analysoit paitsi yhden tietyn tilanteen, jossa jaetaan tietyt kaksi korttia, myös saat yleiskuvan siitä, miten tällaisessa tilanteessa tulisi pelata kaikilla muilla korteilla.
Jos yhdessä tilanteessa teet panostuksen arvon vuoksi, rangesi tulisi sisältää myös kortteja, joilla bluffaisit samassa paikassa, jolloin vastustajasi ei koskaan voi olla varma, bluffaatko vai onko sinulla vahva yhdistelmä. Jos panostat riverillä vain silloin, kun sinulla on vahva käsi, vastustaja voi aina kannattavasti foldata, koska tietää, ettet koskaan bluffaa tällaisessa tilanteessa. Toisaalta, jos bluffaat tällaisissa tilanteissa liian usein, vastustaja voi aina kannattavasti maksaa, koska tietää, että sinulla ei juuri koskaan ole vahvaa kättä.
Jos et vieläkään usko, että GTO:hon perustuva strategia on oikea tie, nämä hypoteettiset Doug Polkin esimerkit saattavat auttaa.
Pokeriteoria, esimerkkejä
Riverillä panostat 100 dollaria 100 dollarin pottiin, joten vastustajasi täytyy maksaa 100 voittaakseen 200 potin. Tämä tarkoittaa, että vastustajallasi on 2:1 pot odds ja hänen täytyy voittaa vähintään 33 % kerroista ollakseen omillaan.
Tämä lyhyt laskelma osoittaa optimaalisen bluffien osuuden rangessasi, kun panostat riverillä. Joten 33 % tarkoittaa, että bluffaat kerran kolmesta ja panostat arvon vuoksi kaksi kertaa kolmesta. Tämä taajuus on optimaalinen, koska useimmiten voitat potin etkä riskeeraa tulla paljastetuksi.
Katsotaanpa neljää eri panostuksen arvon ja bluffin suhteen skenaariota, jotka auttavat ymmärtämään, miksi 33 % bluffeja ja 67 % arvon vuoksi panostuksia sisältävä range on optimaalinen ja miksi vastustajasi eivät voi tehdä sinulle mitään.
Skenaariot yksinkertaistetaan, kuvitellaan, että aina voitat, kun vastustaja maksaa arvon vuoksi panostuksesi ja aina häviät, kun hän maksaa bluffisi.
1. skenaario – bluffi 0 %, arvon vuoksi panostus 100 %
Vastustajasi voi foldata 100 % kerroista. Tuloksissasi tämä näkyy siten, että voitat 100 dollaria panostusrangellasi.
2. skenaario – bluffi 100 %, arvon vuoksi panostus 0 %
Vastustajasi voi maksaa 100 % kerroista. Tuloksissasi tämä näkyy siten, että häviät 100 dollaria panostusrangellasi.
3. skenaario – bluffi 50 %, arvon vuoksi panostus 50 %
Jos vastustajasi maksaa 100 % kerroista, voitat aina 200 dollaria, kun panostat arvon vuoksi, ja häviät 100 dollaria, kun bluffaat. Tuloksissasi tämä näkyy siten, että voitat 50 dollaria, jos vastustaja aina maksaa. (50 % * -$100 = -$50; 50 % * $200 = $100. $100 – $50 = $50).
Jos vastustaja aina foldaa, voitat 100 dollaria (kuten ensimmäisessä skenaariossa)
Tämä skenaario osoittaa, että bluffaamatta jättäminen on yhtä kannattavaa kuin bluffata 50 % kerroista.
4. skenaario – bluffi 33 %, arvon vuoksi panostus 67 %
Jos vastustajasi aina maksaa, voitat 200 dollaria, kun panostat arvon vuoksi, ja häviät 100 dollaria aina, kun bluffaat. Tässä tapauksessa häviät 100 dollaria vain 33 % kerroista ja voitat 200 dollaria 67 % kerroista, mikä tarkoittaa, että voittosi on 100 dollaria. (33 % * $100 = -$33; 67 % * $200 = $133. $133 – $33 = $100).
Tällainen bluffien ja arvon vuoksi panostusten suhde on optimaalinen, koska:
- Voitat 100 dollaria, jos vastustajasi aina maksaa
- Voitat 100 dollaria, jos vastustajasi aina foldaa
Joten ansaitset 100 dollaria riippumatta siitä, mitä vastustajasi tekee. Tietenkin tämä win-win-skenaario on mahdollinen vain, kun rangesi on täydellisesti tasapainotettu. Joten sinulle ei ole väliä, mitä vastustajasi valitsee, koska molemmissa tapauksissa ansaitset yhtä paljon.
Tällaisen tasapainon soveltaminen vastustajien virheiden ja heikkouksien huomioon ottamiseksi voi olla vielä kannattavampaa, mutta se vaatii luotettavaa tietoa vastustajasta ja oikeaa soveltamista. Jos haluat nousta tasoilla ja pitkällä aikavälillä murskata vastustajasi, GTO on välttämätön.
4 syytä, miksi kannattaa käyttää tätä strategiaa
Katsotaanpa GTO:n hyötyjä strategiassamme, 4 asiaa, jotka saavutamme sisällyttämällä tämän teorian peliimme.
Vältät epäloogista ajattelua
90-luvun pokeriopetuksen perintö – yrittää ymmärtää, millä tasolla pelaaja pelaa.
- Taso, jossa pelaaja ajattelee vain omaa kättään
- Seuraavaksi aletaan pohtia, mitä vastustajalla voisi olla
- Seuraava taso – pohditaan, mitä vastustaja ajattelee sinun korteistasi
- Seuraavaksi alkaa ajattelu siitä, mitä sinä ajattelet, että vastustaja ajattelee, että sinä ajattelet, että hänellä on
- Ja niin edelleen.
Ihannetapauksessa selvität jotenkin, millä tasolla ajattelu päättyy, määrität, millä tasolla vastustaja on ja mukautat sen mukaan. Mutta todellisuus on erilainen ja tason määrittäminen pelatessa heikkoa pelaajaa vastaan on erittäin epäluotettavaa. Ja hyviä ja kokeneita pelaajia vastaan tämä prosessi voi teoriassa jatkua maailmanloppuun asti, kunnes joku toinen yliajattelee toisen.
Tässä on hyvä esimerkki, jossa kaksi pokerilegendaa tasapainottelee.
https://www.youtube.com/watch?v=-hVwpaDH0Xo
En koskaan kyseenalaistaisi Patrik Antoniuksen pokeritaitoja, mutta tällaisia tilanteita voidaan välttää perustamalla bluffausstrategia GTO:hon, joka auttaa välttämään tasosodat, jotka aiheuttavat hämmennystä ja johtavat tilanteisiin, joissa bluffaat ilman equityä.
Vältät virheellisiä oletuksia
Toinen etu – kun tarkastelet peliä GTO:n näkökulmasta, vältät virheellisiä oletuksia muista pelaajista. Tietenkin jotkut oletukset ovat mahdollisia, jos sinulla on enemmän kuin tarpeeksi pelattuja käsiä tiettyä pelaajaa vastaan, mutta hyvin yleistävät oletukset voivat maksaa paljon.
Esimerkiksi ei olisi viisasta sanoa “tässä EI KOSKAAN ole bluffia” tai “hän AINA bluffaa tässä”. Ei myöskään pitäisi ajatella, että tuntematon vastustaja ei voi omistaa tiettyä kättä omassa range:ssään tai että hän avaa hyvin kapeasti tai hyvin laajasti.
Hyvin rakennettu GTO-strategia poistaa hämmennyksen pelistäsi ja auttaa pelaamaan kannattavaa pokeria pitkällä aikavälillä.
Objektiivinen analyysi
Useimmat pelaajat syyttävät itseään huonosti pelatusta kädestä vain siksi, että he eivät onnistuneet voittamaan sitä. Kuitenkin kehittyessäsi ja edetessäsi pokeriurallasi alat ymmärtää, että pokeri ei ole sellainen liiketoiminta, jonka tuloksia voidaan arvioida tyhjiössä.
Objektiivinen ajattelu voi olla erittäin vaikeaa, erityisesti silloin, kun pelatun käden tulos on erittäin huono tai erittäin hyvä. Se, että sait riverillä täyskäden ja voitit paljon merkkejä vastustajaltasi, ei tarkoita, että kaksi kertaa vastustajan panostukseen vastaaminen oli hyvä peli.
Kun selvität, mikä päätös on kannattavin GTO:n mukaan tietyssä tilanteessa, sisällytä käsi istuntoanalyysiisi nähdäksesi, teitkö pitkällä aikavälillä kannattavan päätöksen ei vain tietyn käden, vaan koko range:si kanssa.
Kaikki menestyvät pokerinpelaajat tietävät, että omien virheiden myöntäminen on välttämätöntä, jos haluat pelata hyvin. GTO tarjoaa perustan, joka auttaa havaitsemaan virheet paljon helpommin.
Helpompi sopeutuminen
Miksi teoria on tärkeä, kun yritetään sopeutua muihin pelaajiin? Tehdäksemme asian yksinkertaisemmaksi, pelataan peliä.
Kuvittele, että olet unohtanut kaiken, mitä tiesit pokeristrategiasta, paitsi perustiedot pelistä, ja pelaat ensimmäistä kättä elämässäsi.
Live-peli, pakolliset panokset $1/$2, tehokas pino $200.
Sankari saa Ad9d ja on BB-asemassa. Kaikki foldaavat BTN:lle asti, BTN korottaa $7:ään. SB foldaa, sankari maksaa.
Floppi (potissa $14) As Td 3h
Sankari checkaa, BTN panostaa $9, sankari maksaa.
Turn (potissa $32) Jc
Sankari checkaa, BTN panostaa $21, sankari maksaa.
River (potissa $74) 9c
Sankari checkaa, BTN panostaa $50, sankari maksaa.
BTN näyttää Ah 2c. Sankari voittaa $174 kahdella parilla.
Mitä teet seuraavalla kerralla, kun kohtaat tämän pelaajan tällaisessa tilanteessa, kuinka voit muuttaa peliäsi hyödyntääksesi vastustajan heikkoutta? Ilman teoreettista ymmärrystä tästä tilanteesta et tiedä, mistä aloittaa.
Toisaalta, jos tiedät, miten teoreettisesti parhaiten pelata A2o BTN-asemassa, tiedät myös, miten vastustajasi poikkeaa siitä. Tämä tieto yksinkertaistaa sopeutumista tähän vastustajaan.
Tässä ovat erityiset muutokset, joita voimme tehdä murskataksemme vastustajan aggressiivisen thin value -strategian.
- Pieni hyväksikäyttö. Vastaa vastustajan panostuksiin laajemmin (heikommilla yhdistelmillä kuin tavallisesti) kaikilla kaduilla, kun hän panostaa. (älä liioittele)
- Suuri hyväksikäyttö. Hyökkää armottomasti hänen checkaus range:aan, kun hän on selvästi hyvin heikko, suurilla panostuksilla sekä thin value -käsillä että kohtuullisella määrällä bluffeja.
Hyvin usein optimaalisen pelin teorian ymmärtäminen auttaa helpommin hyödyntämään vastustajien heikkouksia, koska tiedät tarkalleen, missä vastustajasi päätökset poikkeavat optimaalisesta pelistä. Kun et tiedä, mikä on hyvää, on lähes mahdotonta ymmärtää, mikä on huonoa.
Yhteenveto
Täydellisen GTO-strategian tavoittelu saattaa tuntua loogiselta johtopäätökseltä, mutta totuus on, että kukaan ei pysty pelaamaan täydellisesti tämän teorian mukaan. Pokeri ratkaistaan joskus ihmisen tai koneen toimesta, mutta suosittelemme silti perustamaan pelisi tähän teoriaan niin paljon kuin mahdollista. Kuten aina, tämä tarkoittaa, että sinun on työskenneltävä pelisi parissa sekä pelatessasi että pelin ulkopuolella.
Tämä artikkeli on vain yhteenveto peliteorian perusteista, joita sovelletaan pokerissa, mutta toivomme, että sait siitä jotain hyödyllistä tai ainakin herätit uteliaisuutesi – kuinka rikastuttaa peliäsi soveltamalla peliteoriaa.