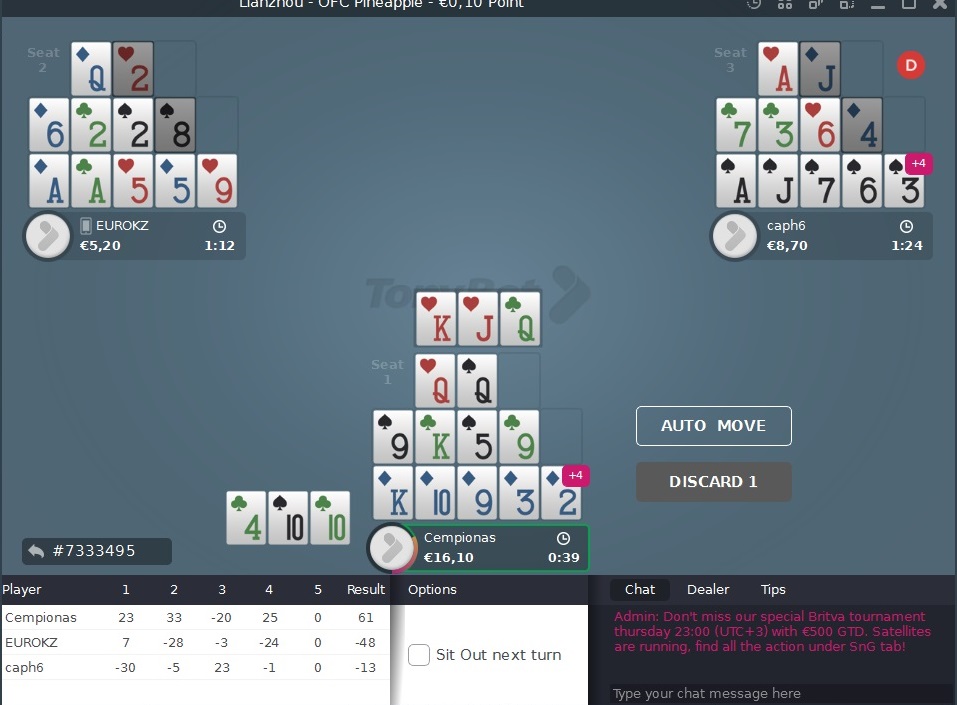
A specific example from my game. When I place these cards, only the last deal, the last three cards, will remain, so before making a decision, I need to know very well if it is worth it for me. In this case, the bottom is already set, it is obvious that 9 will go to the middle, but what to do with Q? After all, we only have one draw left and we are blocking one K ourselves. Should we put Q on top and take the risk? Or is it better to choose a safer line? I think many players are familiar with this situation and often we don't even have that 9. We only have Q and the question is whether to take the risk when only two Ks are left. So let's try to calculate these situations together with you.
First question: how many outs do we have? Outs are all the cards that suit us, which can make our combination a winning one.
If we place QQ on top, we need to put something stronger than QQ in the middle, so all the remaining cards, both K, 9, or 5, are suitable for us. We need to count how many cards are left for us in total. There are two free Ks left. All the nines are out. There is still one five left, despite the fact that we have three live cards, we need to remember that both opponents have discarded two cards each, which we do not see. Usually, high cards like A/K/Q are not discarded because they are used to collect fantasy or strengthen the second line, but smaller cards, in this case, 5, which are completely unnecessary for our opponents, one of them could have definitely discarded it. So, we counted that we have 2-3 outs. What is the next step? We need to find out how many outs have %, i.e., what is the probability that one of those cards will fall to us. Most players, especially those who have played other types of poker, will say that 2-3 outs are nothing, but let's not rush to judge.
How many cards are left in the deck? We play with a total of 52 cards. So, both opponents have dealt 9 cards each and discarded 2 each. In this case, after our move, we will have already dealt 11 cards and discarded 3, so a total of 9+9+2+2+11+3 = 36 cards are out. In other words, there are 52-36 = 16 cards left in the deck.
What is the winning %? So, knowing how many cards suit us and how many are left, it is easy to calculate our winning %. The simplest way to do this is with the following formula.
1 – (A/Z) x (A/Z) x (A/Z) =
A – unsuitable cards for us
Z – all remaining cards
don't be afraid, this is the simplest formula that could be in all of mathematics.
Let's go back to our specific example:
There are 16 cards left in the deck. So Z = 16.
The suitable cards for us are 3, and the unsuitable cards are 16-3 = 13. So A = 13. And the whole action is repeated three times because we get three cards in hand, i.e., our probability increases if we don't draw the needed K or 5 with the first card, maybe it will be the second card or even the third. So let's try to put everything into our formula.
1 – (13/16) x (12/15) x (11/14) =
The first time we had 13/16, but in the second action, we already have one card less because we drew one. So, we have 12/15 left, and in the third action even less, i.e., when drawing the third card, there will be only 14 cards left in the deck and 11 of them will be unsuitable.
Let's try to get %. For those for whom division is too complicated, you can use online calculators like this one: http://calculator.tutorvista.com/multiplying-3-fractions-calculator.html
1 – (13/16) x (12/15) x (11/14) = 0.489 = ~49%.
So, we counted all the remaining cards, counted the suitable ones for us, and managed to find out what the probability is that we will draw a suitable card. In this situation, we have ~49% to draw one of the suitable cards. Quite a lot, right?
Simple formula, simple calculations, stunning results 🙂
To make your work even easier, I am adding an outs table. Just note that our % differs from our position. The later our position, the fewer cards are left in the deck, the higher the probability of drawing a suitable card.
Our analyzed situation -> First position -> 16 cards left
1 out: 18.7%
2 outs: 35%
3 outs: 49%
4 outs: 60.7%
5 outs: 70%
6 outs: 78.6%
Middle position -> 13 cards left
1 out: 23.1%
2 outs: 42.3%
3 outs: 58%
4 outs: 70.6%
5 outs: 80.4%
6 outs: 87.8%
Late position – dealer – 11 cards left.
1 out: 33.6%
2 outs: 53.33%
3 outs: 70.83%
4 outs: 83.33%
5 outs: 91.66%
6 outs: 96.60%
This is a great start, but poker math doesn't end there. In the next article, we will continue to explore mathematical solutions for Chinese poker, trying to calculate EV.