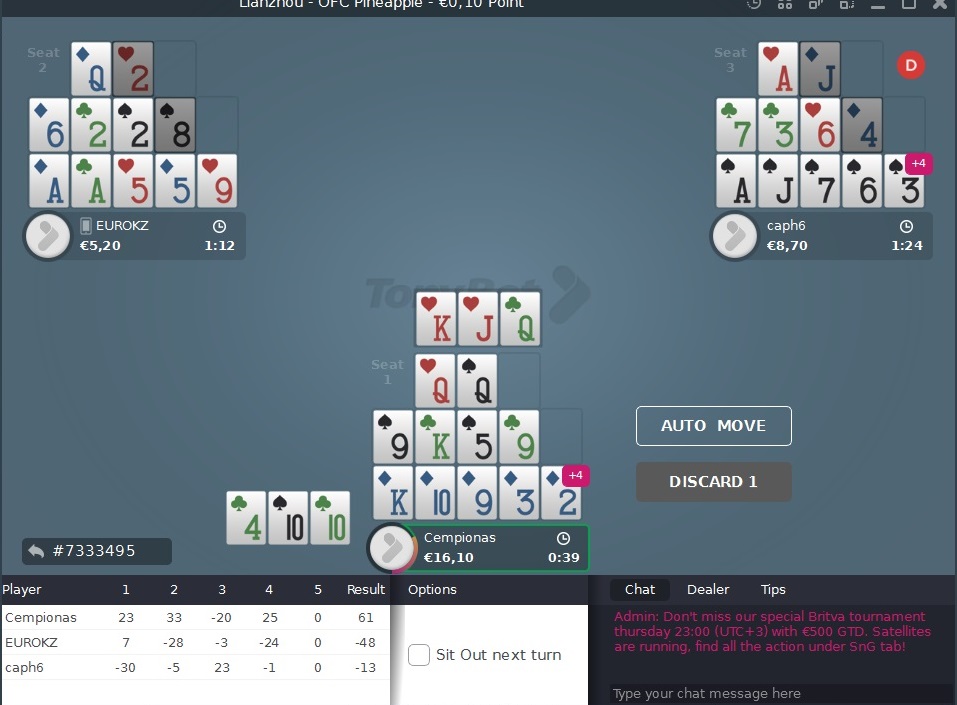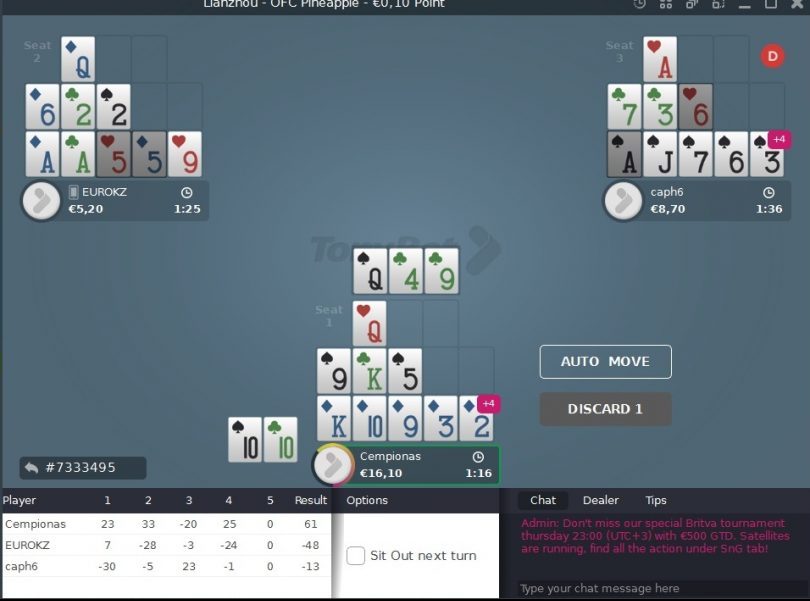
Konkreetti esimerkki omasta pelistäni. Kun asetan nämä kortit, jäljellä on vain viimeinen jako, viimeiset kolme korttia, joten ennen päätöksen tekemistä minun on tiedettävä hyvin, kannattaako se minulle. Tässä tapauksessa alarivi on jo hoidettu, on selvää, että 9 menee keskelle, mutta mitä tehdä Q:n kanssa? Meillä on jäljellä vain yksi nosto ja estämme itseämme yhdellä K:lla. Pitäisikö laittaa Q ylös ja ottaa riski? Vai valita turvallisempi linja? Uskon, että monille pelaajille tämä on hyvin tuttu tilanne, eikä meillä useimmiten ole edes sitä 9:ää. Meillä on vain Q ja kysymys kuuluu, pitäisikö riskeerata, kun jäljellä on vain kaksi K:ta? Yritetään laskea nämä tilanteet yhdessä.
Ensimmäinen kysymys: kuinka monta outtia meillä on? Outit ovat kaikki meille sopivat kortit, jotka voivat tehdä yhdistelmästämme voittavan.
Jos laitamme QQ ylös, meidän on laitettava keskelle jotain vahvempaa kuin QQ, joten kaikki jäljellä olevat kortit, sekä K, 9 että 5, ovat meille sopivia. Meidän on laskettava, kuinka monta korttia meillä on jäljellä. Jäljellä on kaksi vapaata K:ta. Kaikki yhdeksiköt ovat menneet. Jäljellä on vielä yksi viitonen, vaikka meillä on kolme elävää korttia, on muistettava, että molemmat vastustajat ovat heittäneet pois kaksi korttia, joita emme näe. Useimmiten tällaisia korkeita kortteja kuten A/K/Q ei heitetä pois, koska niitä käytetään fantasian keräämiseen tai toisen rivin vahvistamiseen, mutta pienemmät kortit, tässä tapauksessa 5, joka ei ole vastustajillemme tarpeellinen, joku heistä on voinut heittää sen pois. Joten laskimme, että meillä on 2-3 outtia. Mikä on seuraava askel? Meidän on löydettävä, kuinka monta prosenttia outit ovat, eli mikä on todennäköisyys, että saamme yhden näistä korteista. Useimmat pelaajat, erityisesti ne, jotka ovat pelanneet muita pokerin lajeja, sanovat, että 2-3 outtia on täysin merkityksetöntä, mutta älkäämme kiirehtikö tuomitsemaan.
Kuinka monta korttia on jäljellä pakassa? Pelaamme yhteensä 52 kortilla. Joten molemmat vastustajat ovat jakaneet 9 korttia ja heittäneet pois 2 korttia. Tässä tapauksessa, meidän siirron jälkeen olemme jo jakaneet 11 korttia ja heittäneet pois 3, joten yhteensä on mennyt 9+9+2+2+11+3 = 36 korttia. Toisin sanoen pakassa on jäljellä 52-36 = 16 korttia.
Mikä on voittoprosentti? Joten, tietäen kuinka monta korttia meille sopii ja kuinka monta on jäljellä, on helppo laskea voittoprosenttimme. Yksinkertaisin tapa tehdä se on seuraavan kaavan mukaan.
1 – (A/Z) x (A/Z) x (A/Z) =
A – meille sopimattomat kortit
Z – kaikki jäljellä olevat kortit
ei tarvitse pelästyä, tämä on helpoin kaava, mitä matematiikassa voi olla.
Palataanpa konkreettiseen esimerkkiimme:
Pakassa on jäljellä 16 korttia. Joten Z = 16.
Meille sopivia kortteja on 3, ja sopimattomia kortteja 16-3 = 13. Joten A = 13. Ja koko prosessi toistetaan kolme kertaa, koska saamme käteen kolme korttia, eli todennäköisyytemme kasvaa, jos emme saa tarvittavaa K:ta tai 5:ta ensimmäisellä kortilla, se voi olla toinen kortti tai jopa kolmas. Joten yritetään asettaa kaikki kaavaamme.
1 – (13/16) x (12/15) x (11/14) =
Ensimmäisellä kerralla meillä oli 13/16, mutta toisessa vaiheessa meillä on yksi kortti vähemmän, koska yksi on vedetty. Joten meillä on jäljellä 12/15, ja kolmannessa vaiheessa vielä vähemmän, eli kolmatta korttia vedettäessä pakassa on enää 14 korttia ja 11 niistä on sopimattomia.
Yritetään saada prosentit. Jos jakolasku on liian monimutkainen, voit käyttää internetissä olevia laskimia, kuten tätä: http://calculator.tutorvista.com/multiplying-3-fractions-calculator.html
1 – (13/16) x (12/15) x (11/14) = 0.489 = ~49%.
Joten laskimme kaikki jäljellä olevat kortit, laskimme meille sopivat kortit ja pystyimme löytämään todennäköisyyden, että saamme meille sopivan kortin. Tässä tilanteessa meillä on jopa ~49% mahdollisuus saada yksi meille sopivista korteista. Ei huono, eikö?
Yksinkertainen kaava, yksinkertaiset laskelmat, hämmästyttävät tulokset 🙂
Helpottaakseni työtäsi vielä enemmän, lisään outtitaulukon. On vain huomattava, että prosenttimme vaihtelee asemamme mukaan. Mitä myöhäisempi asemamme on, sitä vähemmän kortteja on jäljellä pakassa, ja sitä suurempi on todennäköisyys saada meille sopiva kortti.
Analysoitu tilanne -> Ensimmäinen asema -> jäljellä 16 korttia
1 outti: 18,7%
2 outtia: 35%
3 outtia: 49%
4 outtia: 60,7%
5 outtia: 70%
6 outtia: 78,6%
Keskiasema -> jäljellä 13 korttia
1 outti: 23,1%
2 outtia: 42,3%
3 outtia: 58%
4 outtia: 70,6%
5 outtia: 80,4%
6 outtia: 87,8%
Myöhäinen asema – jakaja – jäljellä 11 korttia.
1 outti: 33,6%
2 outtia: 53,33%
3 outtia: 70,83%
4 outtia: 83,33%
5 outtia: 91,66%
6 outtia: 96,60%
Tämä on hyvä alku, mutta pokerin matematiikka ei lopu tähän. Seuraavassa artikkelissa jatkamme yhdessä kiinalaisen pokerin matemaattisten ratkaisujen tutkimista yrittäen laskea EV:tä.