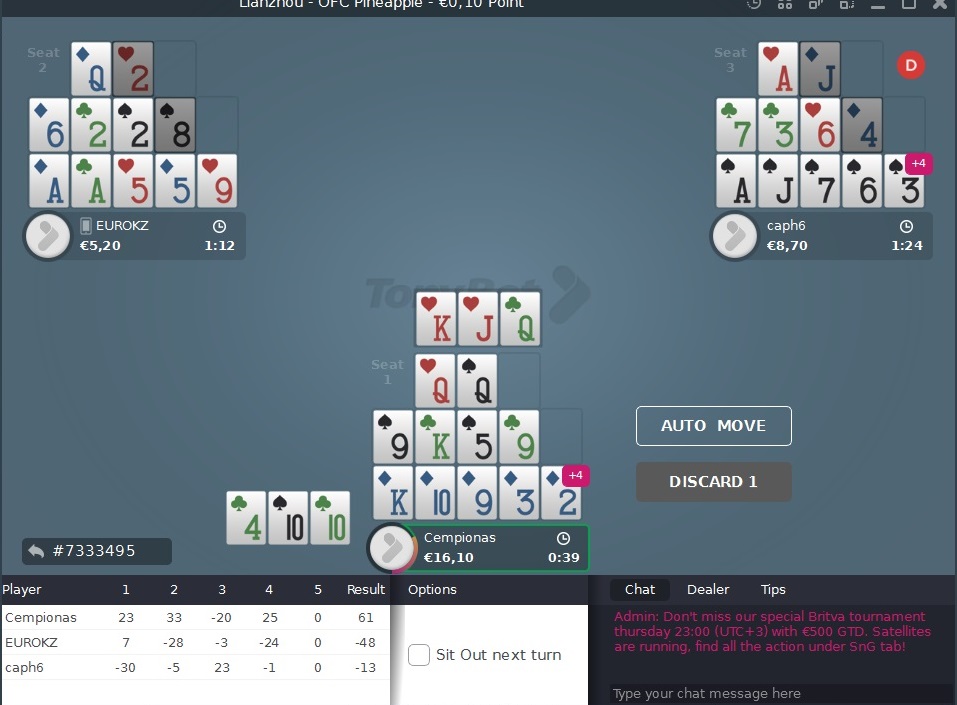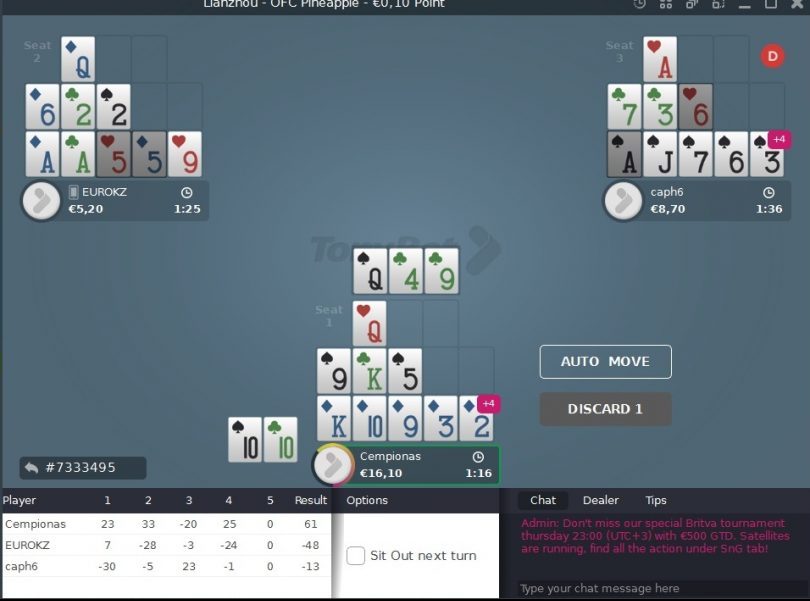
Konkrēts piemērs no manas spēles. Kad izdalīšu šīs kārtis, paliks tikai pēdējā izdalīšana, pēdējās trīs kārtis, tāpēc pirms lēmuma pieņemšanas man ir ļoti labi jāzina, vai tas man ir izdevīgs. Šajā gadījumā apakša mums jau ir sakārtota, pats par sevi saprotams, ka 9 ies vidū, bet ko darīt ar Q? Mums ir palicis tikai viens vilkums un mēs paši bloķējam sev vienu K. Vai likt Q augšā un riskēt? Vai labāk izvēlēties drošāku līniju? Domāju, ka daudziem spēlētājiem šī ir ļoti pazīstama situācija un bieži vien mums pat nav tā 9. Mums ir tikai Q un jautājums, vai riskēt, kad ir palikuši tikai divi K? Tātad mēģināsim kopā ar jums aprēķināt šīs situācijas kopā.
Pirmais jautājums: cik mums ir autu? Auti – visas mums derīgās kārtis, kas var padarīt mūsu kombināciju uzvarētāju.
Ja augšā mēs liksim QQ, vidū mums jāliek kaut kas stiprāks par QQ, tāpēc visas atlikušās kārtis, gan K, gan 9 vai 5, ir mums derīgas, tāpēc jāaprēķina, cik mums ir atlikušās kārtis kopumā. Ir palikuši divi brīvi K /K. Visi devītnieki ir izkrituši. Vēl ir viena pieciniece, neskatoties uz to, ka mums ir trīs dzīvas kārtis, jāatceras, ka abi pretinieki ir izmetuši pa divām kārtīm, kuras mēs neredzam. Parasti tādas augstas kārtis kā A/K/Q netiek izmestas, jo tās tiek izmantotas fantāzijas savākšanai vai otrās līnijas stiprināšanai, bet mazākas kārtis, šajā gadījumā 5, kas mūsu pretiniekiem ir pilnīgi nevajadzīgas, viens no viņiem noteikti varēja to izmest. Tātad, aprēķinājām, ka mums ir 2-3 auti. Kāds ir nākamais solis? Jāatrod, cik auti ir %, t.i., kāda ir varbūtība, ka mums izkritīs viena no tām kārtīm. Lielākā daļa spēlētāju, īpaši tie, kas ir spēlējuši citas pokera veidus, teiks, ka 2-3 auti ir pilnīgs nieks, bet nesteigsimies spriest.
Cik kāršu ir palicis kavā? Kopumā mēs spēlējam ar 52 kārtīm. Tātad, abi pretinieki ir izdalījuši pa 9 kārtīm un vēl pa 2 ir izmetuši. Šajā gadījumā, pēc mūsu gājiena mēs jau būsim izdalījuši 11 kārtis un 3 izmetuši, tātad kopā ir izkritušas 9+9+2+2+11+3 = 36 kārtis. Vai citādi sakot kavā ir palikušas 52-36 = 16 kārtis.
Kāds ir uzvaras %? Tātad, zinot, cik mums der kārtis un cik ir palicis, ir viegli aprēķināt, kāds ir mūsu uzvaras %. Vienkāršākais veids, kā to izdarīt, ir pēc šādas formulas.
1 – (A/Z) x (A/Z) x (A/Z) =
A – mums nederīgās kārtis
Z – visas atlikušās kārtis
nevajag baidīties, tā ir vienkāršākā formula, kāda vien var būt visā matemātikā.
Atgriezīsimies pie mūsu konkrētā piemēra:
Kavā ir palikušas 16 kārtis. Tātad Z = 16.
Mums derīgās kārtis ir 3, bet nederīgās kārtis 16-3 = 13. Tātad A = 13. Un viss process tiek atkārtots trīs reizes, jo mēs rokā saņemam trīs kārtis, t.i., mūsu varbūtība palielinās, ja neizvilksim mums nepieciešamo K vai 5 ar pirmo kārti, tad varbūt tā būs otrā kārts vai pat trešā. Tātad mēģināsim visu ievietot mūsu formulā.
1 – (13/16) x (12/15) x (11/14) =
Pirmo reizi mums bija 13/16, bet otrajā darbībā mums jau ir viena kārts mazāk, jo vienu izvilkām. Tātad, mums palika 12/15, bet trešajā darbībā vēl mazāk, t.i., velkot trešo kārti kavā būs tikai 14 kārtis un 11 no tām būs nederīgas.
Mēģināsim iegūt %. Kam dalīšana ir pārāk sarežģīta darbība, var izmantot internetā pieejamos kalkulatorus, kā šis: http://calculator.tutorvista.com/multiplying-3-fractions-calculator.html
1 – (13/16) x (12/15) x (11/14) = 0.489 = ~49%.
Tātad, aprēķinājām visas atlikušās kārtis, aprēķinājām mums derīgās un spējām atrast, kāda ir varbūtība, ka izvilksim mums derīgu kārti. Šādā situācijā mums ir pat ~49% izvilkt vienu no mums derīgajām kārtīm. Daudz, vai ne?
Vienkārša formula, vienkārši aprēķini, pārsteidzoši rezultāti 🙂
Lai vēl vairāk atvieglotu jums darbu, pievienoju autu tabulu. Tikai jāņem vērā, ka mūsu % atšķiras atkarībā no mūsu pozīcijas. Jo vēlākā ir mūsu pozīcija, jo mazāk kāršu ir palicis kavā, jo lielāka ir varbūtība izvilkt mums derīgu kārti.
Mūsu analizētā situācija -> Pirmā pozīcija -> palikušas 16 kārtis
1 auts: 18.7%
2 auti: 35%
3 auti: 49%
4 auti: 60,7%
5 auti: 70,%
6 auti: 78,6
Vidējā pozīcija -> palikušas 13 kārtis
1 auts: 23,1%
2 auti: 42,3%
3 auti: 58%
4 auti: 70,6%
5 auti: 80,4%
6 auti: 87,8%
Vēlā pozīcija – dīleris – palikušas 11 kārtis.
1 auts: 33,6%
2 auti: 53.33%
3 auti: 70.83%
4 auti: 83,33%
5 auti: 91,66%
6 auti: 96,60%
Tas ir lielisks sākums, taču pokera matemātika ar to nebeidzas. Nākamajā rakstā turpināsim analizēt matemātiskos ķīniešu pokera risinājumus, mēģinot aprēķināt EV.