
Game theory belongs to the field of mathematics. Games in this context have a very broad meaning. Essentially, it is a theory that analyzes any situations in which rational agents (usually people) act according to a set (or predictable) strategy. From this definition alone, it is easy to determine the application of GTO concepts in poker.
TOP poker rooms
One of the most well-known and important principles in poker game theory is Nash equilibrium. Many poker players know this concept only from tables that are Push/Fold All in preflop. These tables usually indicate at how many BBs it is possible to shove or call All in against one player. Of course, such tables can be created for a larger number of players, but this is usually not as easy (or useful).
GTO in poker – Nash equilibrium
Nash equilibrium first appeared in poker in the form of well-known “preflop All in” tables, as this is the easiest state to calculate in the game. The fewer chips and players remain, the fewer possible decisions (theoretically) each of them can make.
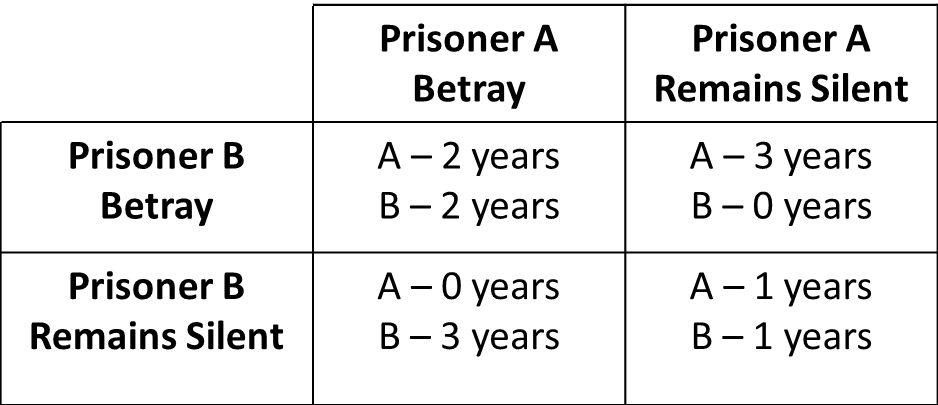
To better understand how the calculation of these situations came about, it is necessary to understand what state is considered Nash equilibrium. Nash equilibrium is a state of the game that is achieved when the following conditions exist:
- There are at least two players.
- A non-cooperative game is played (one in which players can win something at the expense of others).
- All players' strategies are known.
- Strategies are formed in such a way that no player can win more by changing only their strategy.
The fourth point is the most important in this case. Nash equilibrium describes a strategy in which all players play optimally. In poker terms, it is a plan of action such that changing only it cannot win more EV. In poker, Nash Equilibrium would mean 0 EV for all players.
John Forbes Nash, the discoverer of this equilibrium, has proven a very important phenomenon – the theory of the existence of Nash equilibrium. This theorem states that Nash Equilibrium can be found in all games where the number of decisions is not infinite and the winnings correlate with the players' actions (or provide an incentive to create a strategy based on some principles). This means that Nash Equilibrium exists not only in tables but in the entire poker game from preflop to the last river decision. For any poker strategy that has at least one rule, there is a GTO solution that would manifest as a unilateral Nash equilibrium. We will discuss the search for such Game Theory Optimal poker solutions in the next part of this article. Such strategies can already be found with the offered solvers. So, GTO is not just for “top top regs”.
GTO and Nash Equilibrium myths
As mentioned earlier, we usually hear about Nash Equilibrium in poker only when talking about preflop tables, and GTO only when talking about solvers or as some very distant and abstract strategy. In fact, these concepts are applicable to all levels of poker.
Why were Nash tables created first before starting to create and talk about more complex GTO strategies? First, as is well known, these tables are best applied at very low effective stack sizes. The fewer chips, the fewer possibilities both pre and postflop. The importance of postflop when deep also contributes to this reason. Many players do not like to open shove AA at every opportunity.
Second, a much more important reason is the simplification of the game. Nash equilibrium requires understanding at least one player's strategy fully, which in many poker situations is not realistic. Many recreational players probably only have the beginnings of a strategy instead of rational game rules. For this reason, achieving Nash equilibrium in poker was only possible by simplifying the game.
GTO solvers and other modern programs allow calculating a strategy that approaches Nash equilibrium. The best solvers, however, still do not achieve perfection, but for many players, this is not important. The average exploitability per pot does not reach 0.1%, so in poker practice, this means nothing, as players will not be able to memorize all possible GTO strategies. The most important practical and theoretical aspect of GTO and solvers is the formulation of a perfect counter-strategy. For any poker strategy, an optimal, maximum EV strategy can be found. This strategy will be maximally profitable until the other player changes it.
Of course, to start even the simplest optimal strategies, it is necessary to know about the opponent's playing style. It would be best to know specific rules, as these can greatly affect the final result. For example, if we had two players, one who in position 100% flops top pair c-bets ½ pot size, and another who in position bets only 50% flops cbet (with better kickers), even if all their other game rules are identical, the optimal strategies will differ significantly.
GTO in poker – recalculating Nash equilibrium
One of the most important sentences added to all these Nash tables is that it is a simplified poker game. In it, the Small Blind can only go All in or Fold, and the Big Blind can only Call or Fold. Players cannot take any other actions such as Raise and can never go to postflop. This is the main reason why these tables always show Small Blind All in 20+ BB or even higher decisions, although they are usually not applicable in practice.
Finally, many of these tables and decisions are based on the calculations of the book Mathematics of Poker. Contrary to what many players think, we should not blindly apply these tables to our game, as we, especially against recreational players, will never achieve the desired Nash Equilibrium with this table.
A very simple but well-illustrated example is a player who shoves any two cards 25 BB deep. In this case, the tables would be neither close to Nash Equilibrium nor close to maximum EV, as the optimal strategy would be different. The optimal strategy would allow calling wider, as the Small Blind would shove many more bad hands than presented in the decisions.
Changes in Nash equilibrium
Of course, in reality, there will be many more minor deviations from the strategy described in the tables. Spin n Go and HUSNG players know that in the 14-9 BB range Heads Up will be played very differently. Some opponents will limp a lot, some will have more min-raises in their ranges, and so on. Due to these differences, the optimal shove/fold range will always differ quite significantly, so such situations should always be reviewed in ICMizer, especially from the BB perspective. Of course, in situations where a player is encountered only once, intuition or other simplifications of the situation may have to be used.
This is a very old video about Nash changes, but it perfectly illustrates how the optimal game should change.
Relying on push/fold tables can be done as the game approaches 1 BB effective stacks, as all possible strategies approach Nash Equilibrium. Except for the strategy “fold everything,” most strategies at 2, 3, 4, or 5 big blinds will be almost identical or differ very slightly.
So, in this article, we discussed the basics of GTO in poker and the most well-known concept of this theory, Nash Equilibrium. In other articles, more attention will be paid to the search for optimal strategies and the principles of solver operation.





