
Peliteoria kuuluu matematiikan tieteenalaan. Pelit tässä tapauksessa ovat hyvin laajassa merkityksessä. Pohjimmiltaan se on teoria, joka analysoi mitä tahansa tilanteita, joissa rationaaliset toimijat (useimmiten ihmiset) toimivat ennalta määrätyn (tai ennustettavan) strategian mukaisesti. Pelkästään tästä määritelmästä on helppo tunnistaa GTO-konseptien soveltaminen pokerissa.
TOP pokerihuoneet
Yksi tunnetuimmista ja tärkeimmistä periaatteista pokerin peliteoriassa on Nashin tasapaino (tai Nash equilibrium). Monet pokerinpelaajat tuntevat tämän käsitteen vain taulukoista, jotka ovat Push/Fold All in preflop. Näissä taulukoissa on yleensä ilmoitettu, millä BB:llä voi mennä all in tai callata all in ollessaan yhtä pelaajaa vastaan. Tietenkin tällaisia taulukoita voidaan laatia myös suuremmalle pelaajamäärälle, mutta se ei yleensä ole niin helppoa (eikä hyödyllistä).
GTO pokerissa – Nash equilibrium
Nashin tasapaino ilmestyi pokerissa ensimmäisenä tunnetuissa “preflop All in” -taulukoissa, koska se on helpoimmin laskettava tila pelissä. Mitä vähemmän pelimerkkejä ja pelaajia on jäljellä, sitä vähemmän mahdollisia päätöksiä (teoreettisesti) kukin heistä voi tehdä.
Ymmärtääkseen paremmin, miten nämä tilanteet on laskettu, on ymmärrettävä, mikä tila katsotaan Nashin tasapainoksi. Nash equilibrium on pelin tila, joka saavutetaan, kun seuraavat ehdot täyttyvät:
- On vähintään kaksi pelaajaa.
- Peli on ei-yhteistyöpeli (sellainen, jossa pelaajat voivat voittaa jotain toisten kustannuksella).
- Kaikkien pelaajien strategiat ovat tiedossa.
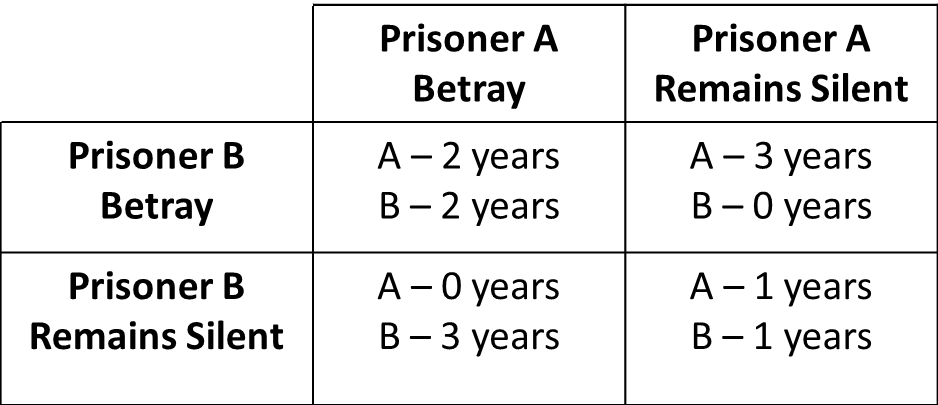
- Muodostetaan sellaiset strategiat, että kukaan pelaaja ei voi voittaa enempää muuttamalla vain omaa strategiaansa.
Neljäs kohta on tässä tapauksessa tärkein. Nash equilibrium kuvaa sellaista strategiaa, jossa kaikki pelaajat pelaavat optimaalisesti. Pokeritermein sanottuna se on sellainen toimintasuunnitelma, että muuttamalla vain sitä ei voi voittaa enempää EV:tä. Pokerin tapauksessa Nash Equilibrium tarkoittaisi 0 EV:tä kaikille pelaajille.
John Forbes Nash, tämän tasapainon löytäjä, on todistanut yhden erittäin tärkeän ilmiön – Nashin tasapainon olemassaolon teorian. Tämä teoreema väittää, että Nash Equilibrium voidaan löytää kaikissa peleissä, joissa päätösten määrä ei ole ääretön ja voitot korreloivat pelaajien toimien kanssa (tai antavat kannustimen luoda jonkinlaisia periaatteisiin perustuvia strategioita). Tämä tarkoittaa, että Nash Equilibrium ei ole olemassa vain taulukoissa, vaan koko pokeripelissä preflopista viimeiseen river-päätökseen. Jokaiselle vähintään yhden säännön omaavalle pokeristrategialle on olemassa GTO-ratkaisu, joka ilmenee yksipuolisena Nash equilibriumina. Tällaisten Game Theory Optimal pokeriratkaisujen etsintää käsitellään tämän artikkelin seuraavassa osassa. Tällaisia strategioita voidaan jo löytää tarjolla olevilla solvereilla. Joten, GTO ei ole vain “top top regseille”.
GTO ja Nash Equilibrium myytit
Kuten aiemmin kirjoitettu, Nash Equilibriumista pokerissa kuullaan useimmiten vain puhuttaessa preflop-taulukoista, ja GTO:sta vain puhuttaessa solvereista tai jonkinlaisena hyvin kaukaisena ja abstraktina strategiana. Todellisuudessa nämä konseptit soveltuvat kaikille pokeritasoille.
Miksi Nashin taulukot luotiin ensin ennen kuin alettiin luoda ja puhua monimutkaisemmista GTO-strategioista? Ensinnäkin, kuten hyvin tiedetään, nämä taulukot soveltuvat parhaiten erittäin matalille effect stack sizeille. Mitä vähemmän pelimerkkejä, sitä vähemmän mahdollisuuksia sekä pre että postflop. Tähän syyhyn liittyy myös postflopin tärkeys syvällä stackilla. Monet pelaajat eitykkäävät open shovata AA aina tilaisuuden tullen.
Toiseksi, paljon tärkeämpi syy on pelin yksinkertaistaminen. Nash equilibrium vaatii ymmärtämään vähintään yhden pelaajan strategian täysin, mikä monissa pokeritilanteissa ei ole realistista. Monet harrastelijapelaajat luultavasti omaavat vain strategian alkeet rationaalisten pelisääntöjen sijaan. Tästä syystä Nashin tasapainon saavuttaminen pokerissa oli mahdollista vain yksinkertaistamalla peliä.
GTO-solverit ja muut modernit ohjelmat mahdollistavat strategian laskemisen, joka lähestyy Nashin tasapainoa. Parhaat solverit eivät kuitenkaan vielä saavuta täydellisyyttä, mutta monille pelaajille se ei ole tärkeää. Keskimääräinen exploitability per pot ei ylitä 0,1%, joten pokerin käytännössä sillä ei ole merkitystä, koska pelaajat eivät pysty muistamaan kaikkia mahdollisia GTO-strategioita. Tärkein GTO:n ja solverien käytännöllinen ja teoreettinen näkökohta on täydellisen vastastrategian muodostaminen. Mihin tahansa pokeristrategiaan voidaan löytää optimaalinen, maksimaalisen EV:n strategia. Tämä strategia on maksimaalisesti tuottoisa, kunnes toinen pelaaja muuttaa sitä.
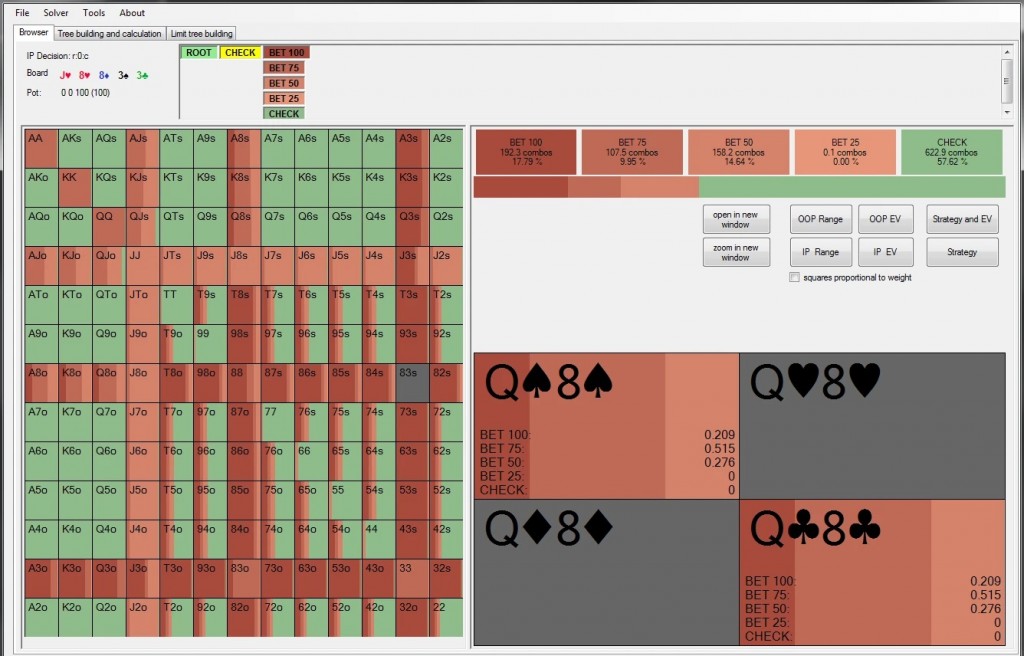
Tietenkin, jotta voisi aloittaa edes yksinkertaisimmat optimaaliset strategiat, on tiedettävä vastustajan pelityyli. Parasta olisi tietää tarkat säännöt, koska nämä voivat vaikuttaa lopputulokseen erittäin paljon. Esimerkiksi, jos meillä olisi kaksi pelaajaa, toinen, joka in position 100% floppaisi top pairin cbettaamalla ½ pot size, ja toinen, joka in position bettaisi vain 50% floppaamalla cbet (paremmilla kickereillä), vaikka kaikki muut heidän pelisääntönsä olisivat identtiset, optimaaliset strategiat eroaisivat huomattavasti.
GTO pokerissa – Nashin tasapainon uudelleenlaskenta
Yksi tärkeimmistä lauseista, jotka lisätään kaikkiin näihin Nashin taulukoihin, on, että se on yksinkertaistettu pokeripeli. Siinä Small Blind voi tehdä vain All in tai Fold, ja Big Blind voi vain Call tai Fold. Pelaajat eivät voi tehdä muita toimia, kuten Raise, eivätkä koskaan voi mennä postflopiin. Tämä on pääsyy siihen, miksi näissä taulukoissa aina näytetään Small Blind All in 20+ BB tai jopa korkeammat päätökset, vaikka ne eivät käytännössä ole usein sovellettavissa.
Lopuksi, monet näistä taulukoista ja päätöksistä on luotu kirjan Mathematics of Poker laskelmien perusteella. Toisin kuin monet pelaajat luulevat, näitä taulukoita ei pitäisi soveltaa sokeasti omaan peliin, koska me, erityisesti harrastelijapelaajia vastaan, emme koskaan saavuta haluttua Nash Equilibriumia näillä taulukoilla.
Erittäin yksinkertainen, mutta tilannetta hyvin havainnollistava esimerkki on pelaaja, joka shovaa mitkä tahansa kaksi korttia 25 BB deep. Tässä tapauksessa taulukot eivät olisi lähelläkään Nash Equilibriumia eivätkä lähelläkään maksimaalista EV:tä, koska optimaalinen strategia olisi erilainen. Optimaalinen strategia sallisi callata laajemmin, koska Small Blind shovaisi paljon enemmän huonoja käsiä kuin taulukoissa esitetyt päätökset.
Nashin tasapainon muutokset
Tietenkin todellisuudessa on paljon enemmän pieniä poikkeamia taulukoissa kuvatusta strategiasta. Spin n Go ja HUSNG-pelaajat tietävät, että 14-9 BB rajoilla Heads Up pelataan hyvin eri tavalla. Jotkut vastustajat limpavat paljon, jotkut lisäävät enemmän minraiseja rangessaan ja niin edelleen. Näiden erojen vuoksi optimaalisin shove/fold range eroaa aina melko paljon, joten tällaiset tilanteet tulisi aina tarkistaa ICMizerilla erityisesti BB:n näkökulmasta. Tietenkin tilanteissa, joissa pelaaja kohdataan vain kerran, voi joutua käyttämään intuitiota tai muita tilanteen yksinkertaistuksia.
Tämä on hyvin vanha video Nashin muutoksista, mutta se havainnollistaa hyvin, miten optimaalisen pelin tulisi muuttua.
Push/fold-taulukoihin voi luottaa pelin lähestyessä 1 BB effective stackeja, koska kaikki mahdolliset strategiat lähestyvät Nash Equilibriumia. Lukuun ottamatta strategiaa “kaikki fold”, useimmat strategiat 2, 3, 4 tai 5 big blindilla ovat lähes identtisiä tai eroavat hyvin vähän.
Joten tässä artikkelissa käsittelimme GTO:n perusteita pokerissa ja tunnetuinta tämän teorian käsitettä Nash Equilibriumia. Seuraavissa artikkeleissa keskitytään enemmän optimaalisten strategioiden etsintään ja solverien toimintaperiaatteisiin.





