
La teoria dei giochi appartiene al campo delle scienze matematiche. I giochi in questo caso hanno un significato molto ampio. Essenzialmente, è una teoria che analizza qualsiasi situazione in cui attori razionali (di solito persone) agiscono secondo una strategia stabilita (o prevedibile). Solo da questa definizione è facile determinare l'applicazione dei concetti GTO nel poker.
TOP sale da poker
Uno dei principi più noti e importanti nella teoria dei giochi del poker è l'equilibrio di Nash (o Nash equilibrium). Molti giocatori di poker conoscono questo concetto solo dalle tabelle che sono Push/Fold All in preflop. Queste tabelle di solito indicano a quanti BB è possibile andare all-in o chiamare all-in contro un singolo giocatore. Naturalmente, tali tabelle possono essere create anche per un numero maggiore di giocatori, ma di solito non è così facile (e utile).
GTO nel poker – Nash equilibrium
L'equilibrio di Nash è apparso per la prima volta nel poker sotto forma delle ben note tabelle “preflop All in”, poiché è lo stato più facilmente calcolabile nel gioco. Meno gettoni e giocatori rimangono, meno decisioni (teoricamente) possono essere implementate da ciascuno di loro.
Per comprendere meglio come è stato calcolato questo stato, è necessario capire quale stato è considerato equilibrio di Nash. Il Nash equilibrium è uno stato del gioco che si raggiunge quando esistono le seguenti condizioni:
- Ci sono almeno due giocatori.
- Si gioca un gioco non cooperativo (in cui i giocatori possono vincere qualcosa a spese degli altri).
- Le strategie di tutti i giocatori sono conosciute.
- Si formano strategie tali che nessun giocatore può vincere di più cambiando solo la propria strategia.
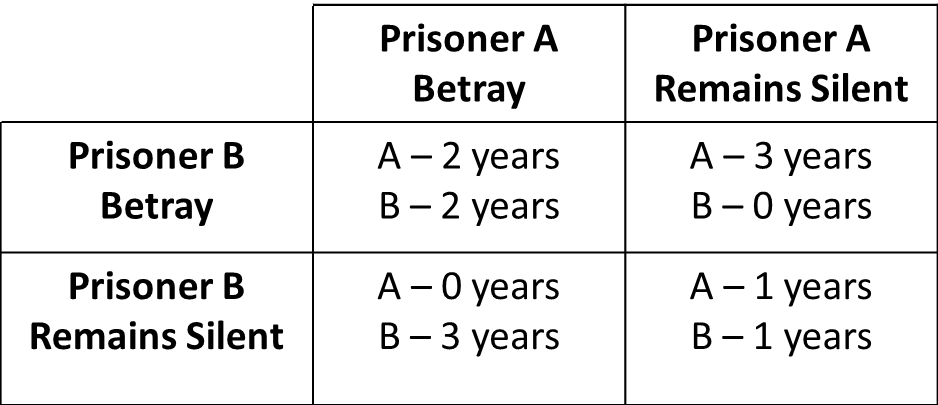
Il quarto punto è il più importante in questo caso. L'equilibrio di Nash descrive una strategia in cui tutti i giocatori giocano in modo ottimale. In termini di poker, è un piano d'azione tale che cambiando solo esso non è possibile vincere più EV. Nel caso del poker, il Nash Equilibrium significherebbe 0 EV per tutti i giocatori.
John Forbes Nash, il scopritore di questo equilibrio, ha dimostrato un fenomeno molto importante: la teoria dell'esistenza dell'equilibrio di Nash. Questo teorema afferma che il Nash Equilibrium può essere trovato in tutti i giochi in cui il numero di decisioni non è infinito e le vincite sono correlate alle azioni dei giocatori (o forniscono un incentivo a creare una strategia basata su alcuni principi). Ciò significa che il Nash Equilibrium esiste non solo nelle tabelle, ma in tutto il gioco del poker, dal preflop all'ultima decisione sul river. Per ogni strategia di poker che ha almeno una regola, esiste una soluzione GTO che si manifesterebbe come unilaterale Nash equilibrium. La ricerca di tali soluzioni Game Theory Optimal nel poker sarà discussa nella prossima parte di questo articolo. Tali strategie possono già essere trovate con i solver proposti. Quindi, il GTO non è solo per i “top top reg”.
Miti su GTO e Nash Equilibrium
Come scritto in precedenza, sentiamo parlare di Nash Equilibrium nel poker principalmente quando si parla di tabelle preflop, e di GTO solo quando si parla di solver o come di una strategia molto lontana e astratta. In realtà, questi concetti sono applicabili a tutti i livelli di poker.
Perché sono state create prima le tabelle di Nash prima di iniziare a creare e parlare di strategie GTO più complesse? Innanzitutto, come è ben noto, queste tabelle sono meglio applicabili con stack size molto bassi. Meno gettoni ci sono, meno possibilità ci sono sia pre che postflop. A questa ragione si aggiunge l'importanza del postflop quando si è deep. Molti giocatori non amano open shovare AA ogni volta che ne hanno l'opportunità.
In secondo luogo, una ragione molto più importante è la semplificazione del gioco. Il Nash equilibrium richiede di comprendere la strategia di almeno un giocatore completamente, il che non è realistico in molte situazioni di poker. Molti giocatori ricreativi probabilmente hanno solo abbozzi di strategia invece di regole di gioco razionali. Per questo motivo, raggiungere l'equilibrio di Nash nel poker è stato possibile solo semplificando il gioco.
I solver GTO e altri programmi moderni permettono di calcolare una strategia che si avvicina all'equilibrio di Nash. I migliori solver, tuttavia, non raggiungono ancora la perfezione, ma per molti giocatori non è importante. L'exploitability medio per pot non raggiunge lo 0,1%, quindi nella pratica del poker non significa nulla, poiché i giocatori non saranno in grado di memorizzare tutte le possibili strategie GTO. L'aspetto pratico e teorico più importante del GTO e dei solver è la formulazione di una controstrategia perfetta. Per qualsiasi strategia di poker è possibile trovare una strategia ottimale, massima EV. Questa strategia sarà massimamente redditizia finché l'altro giocatore non la cambierà.
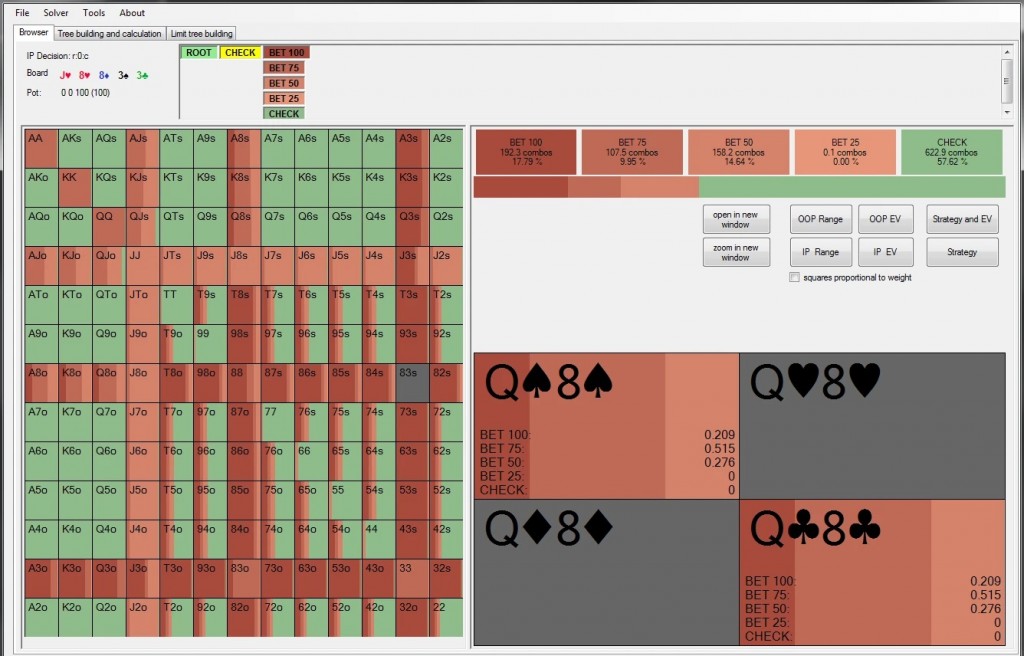
Naturalmente, per iniziare anche le strategie ottimali più semplici, è necessario conoscere lo stile di gioco dell'avversario. Sarebbe meglio conoscere le regole specifiche, poiché queste possono influenzare molto il risultato finale. Ad esempio, se avessimo due giocatori, uno che in posizione floppa il top pair e c-betta ½ pot size, e l'altro che in posizione betta solo il 50% delle volte con top pair (con kicker migliori), anche se tutte le altre loro regole di gioco fossero identiche, le strategie ottimali sarebbero molto diverse.
GTO nel poker – Ricalcolo dell'equilibrio di Nash
Una delle frasi più importanti che vengono aggiunte a tutte queste tabelle di Nash è che si tratta di un gioco di poker semplificato. In esso, lo Small Blind può fare solo All in o Fold, mentre il Big Blind può solo chiamare o foldare. I giocatori non possono fare altre azioni come Raise e non possono mai andare al postflop. Questa è la ragione principale per cui queste tabelle mostrano sempre decisioni di All in dello Small Blind con 20+ BB o anche più alte, anche se nella pratica di solito non sono applicabili.
Infine, molte di queste tabelle e decisioni sono state create basandosi sui calcoli del libro Mathematics of Poker. Contrariamente a quanto pensano molti giocatori, non dovremmo applicare ciecamente queste tabelle al nostro gioco, poiché noi, specialmente contro giocatori ricreativi, non raggiungeremo mai il desiderato Nash Equilibrium con queste tabelle.
Un esempio molto semplice, ma che illustra bene la situazione, è un giocatore che shova qualsiasi due carte con 25 BB deep. In tal caso, le tabelle non sarebbero né vicine al Nash Equilibrium né vicine al massimo EV, poiché la strategia ottimale sarebbe diversa. La strategia ottimale permetterebbe di chiamare più ampiamente, poiché lo Small Blind shoverebbe molte più mani deboli rispetto a quelle indicate nelle decisioni.
Cambiamenti nell'equilibrio di Nash
Naturalmente, nella realtà ci saranno molte più piccole deviazioni dalla strategia descritta nelle tabelle. I giocatori di Spin n Go e HUSNG sanno che nelle fasce 14-9 BB Heads Up si giocherà in modo molto diverso. Alcuni avversari faranno molti limp, altri avranno più minraise nei loro range e così via. A causa di queste differenze, il range ottimale di shove/fold sarà sempre, piuttosto significativamente, diverso, quindi dovremmo sempre rivedere tali situazioni con ICMizer, specialmente dalla prospettiva del BB. Naturalmente, nelle situazioni in cui si incontra un giocatore solo una volta, potrebbe essere necessario affidarsi all'intuizione o ad altre semplificazioni della situazione.
Questo è un video molto vecchio sui cambiamenti di Nash, ma illustra bene come dovrebbe cambiare il gioco ottimale.
Ci si può affidare alle tabelle push/fold man mano che il gioco si avvicina sempre più agli stack effective di 1 BB, poiché tutte le possibili strategie si avvicinano al Nash Equilibrium. A parte la strategia “fold everything”, molte strategie con 2, 3, 4 o 5 big blind saranno quasi identiche o differiranno molto poco.
Quindi, in questo articolo abbiamo discusso le basi del GTO nel poker e il concetto più noto di questa teoria, il Nash Equilibrium. Nei prossimi articoli, ci concentreremo maggiormente sulla ricerca di strategie ottimali e sui principi di funzionamento dei solver.





